Vijčani spoj

Matični vijak: 1. svornjak, 2. navoj, 3. glava, 4. matica.

Glavati vijak sa šesterostranom glavom.

Zatični vijci.

Šesterostrana matica.

Zakrivljena elastična podloška.

Dijelovi za osiguranje vijčanih spojeva povećanjem uzdužne (aksijalne) sile: a) i b) elastičnom podloškom, c) ozubljenom prstenastom podloškom, d) prstenom od stakloplastike usađenim u maticu (sigurnosna matica), e) maticom i protumaticom.

Moment ključ.

Skala na moment ključu.

Hidraulički moment ključu.

Tok sila u vijčanim spojevima: a) spoj s vijkom i maticom.

Tok sila u vijčanim spojevima: b) spoj s utičnim vijkom.

Dijagram naprezanja trgovačkih čelika.

Ispitni uzorak ili epruveta nakon vlačnog ispitivanja. Vidi se suženje promjera uzorka zbog vlačnog istezanja na kidalici.

Elastični vijak.

Očni vijak.

Očni vijak za vješanje tereta.

Ručna vijčana dizalica: 1. poluga, 2. kućište s maticom, 3. vijak.

Prikaz 4 Eulerova modela izvijanja kada nastaje gubitak stabilnosti štapa ili kojega drugog vitkog elementa konstrukcije (na primjer stupa) osno opterećenoga prekomjerno velikom tlačnom silom.

Ručna vijčana dizalica nosivosti 2,5 tone.

Spoj poklopca autoklava.

Autoklav ili Papinov lonac iz 18. stoljeća.

Vijak, matica i ključ.

Dijagram deformacija.

Dijagram dozvoljenih naprezanja σ_{v dop} za vijke (DIN 2507).

Klipni dvoradni kompresor sa 6 cilindara.

Vijci izloženi djelovanju poprečnih sila: a) neprilagođeni vijak, b) prilagođeni vijak.

Sredstva za rasterećenje vijka od poprečnih sila: a) cilindrični prsten, b) zatik, c) stepenasta izbočina.

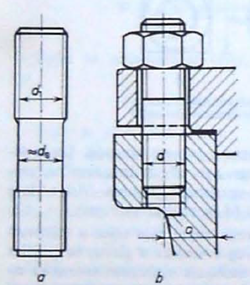
Vijčani spoj spada u rastavljive spojeve, a pored spajanja, koristi se za brtvljenje, zatezanje, regulaciju, mjerenje i prijenos gibanja. Osnovni dijelovi vijčanog spoja su vijak i matica, pri čemu vijak ima vanjski navoj, a matica odgovarajući unutarnji navoj. Matica može u vijčanom spoju biti samostalan dio, ili je zamjenjuje dio spajanog strojnog dijela, u kojemu onda treba izraditi unutarnji navoj. S obzirom na to da su vijak i matica najčešće korišteni strojni dijelovi na svim područjima tehnike, njihov oblik, veličina i materijal su standardizirani.

Vrste vijčanih spojeva

Vijčani spojevi se mogu općenito razvrstati u sljedeće skupine:

• nosivi vijčani spojevi. Najčešći su, a koriste se za pričvršćivanje rastavljivih strojnih dijelova koji su izloženi raznovrsnim naprezanjima. Izvode se s ili bez prednaprezanja;
• dosjedni vijčani spojevi. Koriste se za pričvrsne, rastavljive veze raznih strojnih dijelova dosjednim vijcima, koji dobro podnose smična opterećenja i istovremeno centriraju spajane dijelove. Češće se izvode bez prednaprezanja, a manje s prednaprezanjem;
• pokretni navojni spojevi. Namijenjeni su za prijenos i pretvorbu kružnog gibanja u pravocrtno, ili obrnuto. S njima se postižu velike aksijalne sile za narinute male obodne sile, npr. kod vijčanih vretena alatnih strojeva, u vijčanim dizalicama i slično;
• vijčani spojevi za zatezanje. Koriste se kod zatega s jednim ili dva vijka. Kod zatega s dva vijka jedan vijak ima lijevi, a drugi desni navoj (zatezni vijak);
• brtveni vijčani spojevi. Namjena im je zatvaranje ulaznih i izlaznih otvora posebno oblikovanim vijcima, na primjer kod kliznih ležajeva, u spremnicima i slično;
• diferencijalni vijčani spojevi. Koriste se za podešavanje raznih naprava, te kod regulacije ventila;
• mjerni vijčani spojevi. Služe za mjerenje dužina kod mehaničkih mjerila kao što je mikrometarski vijak.

Prednosti i nedostaci

Prednosti vijčanih spojeva su sljedeći:

• mogu se međusobno spajati svi materijali,
• vijčani spoj se može proizvoljno rastaviti i ponovno sastaviti bez bitnih posljedica za spajane dijelove,
• visoki stupanj standardizacije vijaka i matica osigurava niske troškove nabave i jednostavnu zamjenu,
• nosivost vijčanog spoja sukladna (proporcionalna) je veličini i kvaliteti korištenog vijka i navoja,
• vijčani spojevi vrlo dobro podnose dinamička opterećenja.

Nedostaci vijčanih spojeva su:

• slabljenje presjeka spajanih dijelova i veliko zarezno djelovanje zbog uzdužnog provrta ili provrta s navojem,
• visoka koncentracija naprezanja na mjestima nalijeganja glave vijka ili matice na površinu spajanih dijelova,
• neprestana napregnutost u okolini prednapregnutih vijčanih spojeva.

Pritezanje vijčanog spoja

O pritezanju vijčanog spoja se govori kada se okretanjem matice ili vijka povećava opterećenje vijka. Odvijanjem (odvrtanjem, otpuštanjem) vijčanog spoja rasterećuje se vijak. U nosivim vijčanim spojevima pritezanje se obično podudara s okretanjem matice ili vijka u smjeru zavojnice navoja (uobičajeno je pritezati maticu jer ako se priteže vijak, koji je puno dulji, u početku dolazi do uvijanja ili torzije bez ikakvog pritezanja). Zbog toga se naliježne površine vijka i matice primiču i stišću strojne dijelove koji se spajaju. Način pritezanja i veličina momenta pritezanja od temeljnog su značaja za nosive vijčane spojeve. Nakon pritezanja vijčanog spoja, spajani dijelovi se skraćuju, a istovremeno se vijak rasteže. Kod običnih matica prva dva navoja nose 55 % ukupne sile.

Samokočnost navoja

Samokočnost navoja je ovisna o trenju među navojima i kutu uspona navoja. Kod običnih nosivih vijaka s metarskim normalnim navojem i trokutastim ISO profilom, kut uspona navoja je u području α = 3,6° (M 4) do 1,8° (M 60), dok je reducirani kut trenja među navojima u granicama ρ = 5,2° do 16,1°. Dakle, kod metričkih navoja s trokutastim profilom je kut uspona navoja manji od reduciranog kuta trenja, pa su navoji uvijek samokočni.

Prilikom ocjene veličine pojedinih udjela u pritezanju vijčanog spoja, može se ustanoviti kako je veći dio (80 - 90%) momenta pritezanja vijčanog spoja namijenjen savladavanju trenja među navojima, te između glave vijka ili matice i podloge. Samo manji dio momenta pritezanja stvarno je namijenjen savladavanju sile prednaprezanja, odnosno savladavanju nagiba navoja. Zbog toga je vrlo bitno pravilno odabrati koeficijente trenja.

Kod dinamičkog uzdužnog (aksijalnog) opterećenja s vremenom može doći do loma vijaka zbog zamora na mjestima koncentracije naprezanja, koja su najveća na prvom navojku vijka u matici ili u provrtu s navojem. Kod vijaka s visokim prednaprezanjem lom zbog zamora je vrlo rijedak, jer su vijci opterećeni malim dinamičkim opterećenjima.

Osiguranje vijčanog spoja od odvrtanja

Osiguranje vijčanog spoja od odvrtanja kod statičkih opterećenja nije potrebno, ali se primjenjuje kod dinamičkih opterećenja. Naime, nakon pritezanja vijka dolazi do djelomičnog slijeganja hrapavosti dodirnih površina, može doći do puzanja materijala vijka, a može doći i do lokalnih plastičnih deformacija. Sve to, potpomognuto promjenama opterećenja i eventualnim vibracijama, može rezultirati otpuštanjem vijčanog spoja. U pravilu su dobro proračunati, oblikovani i pritegnuti vijčani spojevi već osigurani protiv neželjenog odvrtanja. To prije svega vrijedi za visokoopterećene spojeve s elastičnim vijcima razreda čvrstoće 8.8 i više, uz male hrapavosti dodirnih površina.

Osiguranje vijčanog spoja od odvrtanja oblikom

Osiguranje oblikom se postiže:

• rascjepkom s običnom ili krunastom maticom; rascjepka prolazi kroz poprečni provrt u vijku
• sigurnosnim limom s izdancima; jedan izdanak se priljubi uz maticu, a drugi savije oko ruba.

Osiguranje vijčanog spoja od odvrtanja silom

Umetanjem posebnih opružnih dijelova se osigurava uzdužna (aksijalna) sila prednapona i pri djelovanju najveće radne sile, makar je došlo do slijeganja hrapavosti ili plastičnih deformacija. Ovi elementi su u obliku rasječenih, zakrivljenih ili tanjurastih prstena (pločica), a izrađeni su od opružnog čelika. Nazivaju se i elastične podloške.

Razne zupčaste i lepezaste prstenaste pločice se svojim zupcima utiskuju u podlogu, povećavaju trenje i tako sprečavaju odvrtanje. Ovakvo osiguranje nije primjenjivo na tvrdim kaljenim površinama. Veće trenje i sprečavanje odvrtanja matice se postiže i sigurnosnom limenom maticom od opružnog čelika koja s unutarnje strane ima više jezičaca koji se zabijaju u navoj. Česta je upotreba dvije matice: kontramatice manje visine koja se priteže na podlogu i normalne matice koja se priteže na kontramaticu (u praksi se često matice pogrešno montiraju obratno!). Matice mogu biti i jednake. Vanjska matica sprečava otpuštanje unutarnje, a na površini njihovog dodira se javlja i dodatno trenje. Za jednokratnu upotrebu se koriste matice s uloškom od umjetne plastične mase u koji vijak urezuje navoj.

Osiguranje vijčanog spoja od odvrtanja materijalom

Vrši se lijepljenjem navoja umjetnim smolama. Često se koristi ljepilo tvrtke "Loctite" kojim se mogu postići vodonepropusni spojevi, na primjer kod spajanja cijevi. Moguće je i zavarivanje glave vijka ili matice za podlogu za što postoje i posebni vijci i matice.

Načini pritezanja vijčanog spoja

Sila u vijku mora prilikom pritezanja biti u dopuštenim granicama da ne bi došlo do plastičnih deformacija ili pucanja vijka.

Ručno pritezanje ključem

Dužina ključa je prilagođena veličini vijka i prosječnoj ručnoj sili, kako moment pritezanja ne bi bio prevelik i doveo do oštećenja vijka. Ova se metoda primjenjuje za vijke korištene za sporedne svrhe.

Pritezanje pneumatskim ili električnim alatom

Moment pritezanja se može grubo podesiti. Služi za serijsko pritezanje vijaka.

Pritezanje momentnim ključem

Preciznije od prethodnih načina je pritezanje momentnim ključem. Kod momentog ključa se jedan njegov dio deformira sukladno veličini momenta pritezanja, dok na drugi neopterećeni dio moment ne djeluje i on se ne deformira. Kod jedne vrste momentog ključa je deformabilni dio torzijska (uvijanje) opruga u obliku šipke na kojoj je i kazaljka. Pri pritezanju se šipka uvija i kazaljka rotira. Kazaljka pokazuje moment pritezanja na skali koja je vezana za drugi neopterećeni dio u obliku cijevi.

Kod jedne druge vrste momentnog ključa se prethodno na skali postavi željeni moment pritezanja. Kad se taj moment postigne, dolazi do međusobnog pomaka nekih dijelova momentnog ključa i čuje se zvučni signal.

Hidrauličko pritezanje

Kod veoma velikih vijaka je pritezanje ključem neprikladno ili nemoguće, jer je moment pritezanja prevelik, a točnost postizanja aksijalne sile u vijku bi bila mala. Takav je slučaj kod vijaka za pričvršćenje poklopaca cilindra velikih motora ili kod preša. Kako sili u vijku odgovara određeno izduženje vijka, hidrauličkim uređajem se vijak izduži, matica se rukom ili podesnim alatom malo pritegne i hidraulički uređaj ukloni. Vijak ostaje izdužen i opterećen silom. Za razliku od prethodnih načina pritezanja, vijak nije opterećen torzijski (uvijanje).

Tok sila, zarezno djelovanje, oblikovanje

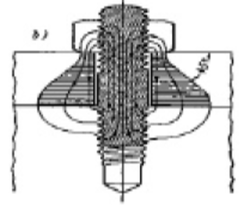
Kod pritezanja vijčanog spoja dolazi do rastezanja vijka, dok spojeni dijelovi bivaju stlačeni. Stvara se zatvoreni tok sila. U vijku nastaje vlačno naprezanje, a u matici i spojenim dijelovima tlačno naprezanje. Tlačna naprezanja vijcima spojenih dijelova ne ograničuju se samo na područje ispod glave vijka, nego se stožasto šire pod 45° do mjesta sastava dijelova. Budući da se matica uzdužno (aksijalno) tlači dok se vijak rasteže, nastaju razlike uspona (koraka) između unutrašnjeg (matica) i vanjskog navoja (vijak), koji prouzročuju progibe pojedinih navoja. Budući da su ti progibi najveći u blizini površina nalijeganja matice i dijelova u spoju, sila se neće jednoliko raspodijeliti, pa nosi obično samo prvih 6 navoja. Nakon što je u prvom navoju dostignuta granica tečenja, u njemu se pri povećanju opterećenja neće više povećavati naprezanje, sve dok se postepeno u svim navojima ne postigne granica tečenja. Povećanje opterećenja vodi, prema tome, k jednoličnijoj raspodjeli sila, ali i nepoželjnoj plastičnoj deformaciji navoja. Nejednolična raspodjela sile smanjuje dinamičku izdržljivost vijaka. Matice u obliku manšete i vlačne matice poboljšavaju raspodjelu sile, jer su djelomično opterećene na vlak.

Visina matice

Podrobniji članak o temi: Matica (naprava)

Nasilnim razaranjem nekog vijčanog spoja preopterećenjem puknut će navoj matice, ili navoj vijka, ili će vijak pući u jezgri. Prva dva slučaja mogu nastati samo ako ima premalo nosivih navoja. Budući da je presjek odreza unutarnjeg navoja (matice) veći od presjeka odreza vanjskog navoja (vijka), lom će nastati najprije u navoju vijka, ako su i vijak i matica od jednakog materijala. Vijčani je spoj izdržljiviji ako se pri preopterećenju ne istrgne navoj, nego se lomi jezgra vijka. To iziskuje minimalnu dubinu uvijanja m (u danom slučaju visina matice m), koja je ovisna o finoći navoja d/P. Prema iskustvu potrebna je dubina uvijanja ili visina matice:

$m\geq (0,175+0,065\cdot {\frac {d}{P}})\cdot d$

Za matice ili konstrukcijske dijelove od lakih metala (na primjer aluminijske legure) preporučuje se m ≥ 2∙d. Visina normalnih šesterostranih matica iznosi m ≈ 0,8∙d. Ako za njih biramo materijal vijka i materijal matice tako da je minimalna čvrstoća σ_M vijka jednaka ispitnom naprezanju σ_vL matice, onda je osigurano da se u slučaju preopterećenja lomi vijak (svornjak), ali ne dolazi do toga da navoj bude istrgnut.

Zbog prevelikog pritezanja vijčanog spoja bokovi navoja se tlače toliko, da se navoj zariba. Ako je najmanja dubina uvijanja (visina matice) održana i ako su vijak i matica, odnosno dijelovi u spoju, izrađeni od materijala različite čvrstoće, ne treba se bojati zaribavanja.

Na svornjaku vijka razlikujemo presjek preko kojeg se prenosi naprezanje A_z, kao stvaran presjek i presjek jezgre A_j kao najuži presjek u snopu silnica. Naziv presjek preko kojeg se prenosi naprezanje zapravo i nije posve opravdan, jer tok silnica ne doseže njegov vanjski rub, pa on zbog toga ostaje bez naprezanja. Na presjek preko kojeg se prenose naprezanja odnose se međutim, lomno naprezanje σ_M i granica tečenja σ_T.

Kod pritezanja se presjek jezgre vijka napreže na vlak i uvijanje (torziju). Vlačno naprezanje povisuje se onda još i pogonskim uzdužnim opterećenjem. Urezani navoji su zarezi koji sprečavaju rastezanje i povećavaju granicu loma i granicu tečenja, ali smanjuju dinamičku izdržljivost.

Utjecaj zareza može se ublažiti:

• povećanjem polumjera zaobljenja R u korijenu navoja;
• izradom vijka i položajem matice koji omogućuju da se ispod prvog nosivog navoja može izvesti jače zaokruženje svornjaka;
• naknadnim valjanjem korijena navoja urezanih, ubrušenih ili uvaljanih navoja, nakon izvršene toplinske obrade (žarenje). Time se stvaraju vlastiti tlačni naponi, koji smanjuju vršna vlačna naprezanja od prednaprezanja i od pogonske sile;
• nitriranjem ili cementiranjem bokova, što također stvara vlastite tlačne napone.

Sve promjene presjeka izazivaju vršna naprezanja, koja rastu s oštrinom prijelaza. Oni se javljaju između struka i navoja i ponekad između struka i glave (struk je dio vijka bez navoja, a svornjak dio koji nosi navoj). Vršna naprezanja nisu tako visoka kao u jezgri, ali mogu postati opasna pri dodatnom naprezanju na savijanje, na primjer pri kosom nalijeganju glave. Vršna naprezanja posve nestaju ako se prijelaz na struk zaobli na a ≧ d. Udarno opterećeni vijci izvode se kao takozvani elastični vijci, koji se od krutih razlikuju po tome što im je struk sužen na d_t = (0,6 - 0,8)∙d. Elastični vijci djeluju radi veće elastičnosti prigušno na udar. Nitriranje, cementiranje ili valjanje korijena povisuje granicu tečenja struka do oko 100%.

Sila prednaprezanja, pritezni moment

Pritezanjem vijka stvara se u presjeku jezgre naprezanje od pritezanja σ_pr. Njegova je veličina u velikoj mjeri ovisna o osjećaju kojim monter priteže vijak pa se dobivena naprezanja rasipaju u širokim granicama.

Očekivanu silu prednaprezanja treba izračunati iz:

$F_{p}=A_{j}\cdot \sigma _{pr}$

gdje je: F_p - sila prednaprezanja (N), A_j - presjek jezgre vijka (mm²), $\sigma _{pr}$ - prednaprezanje (N/mm²) pri pažljivom pritezanju, uz osjećaj da se ne pretegne, obično srednja vrijednost.

Tanki vijci pritegnuti pažljivo prema osjećaju, čvršće su stegnuti nego debeli. Zbog toga za tanke vijke treba upotrijebiti materijale s visokom granicom tečenja. Visoko napregnuti vijčani spojevi kojima se pridaje posebna važnost pritežu se momentnim ključevima, koji iskapčaju pri dosizanju postavljenog momenta pritezanja. Željenu silu prednaprezanja možemo izračunati približno:

$T_{pr}\approx F_{p}\cdot (0,16\cdot P+\mu \cdot {\frac {d_{2}+D_{sr}}{2}})$

gdje je: T_pr - moment pritezanja (Ncm), F_p - potrebna sila prednaprezanja (N), P - uspon ili korak navoja (cm), μ - koeficijent trenja na bokovima navoja i na glavi vijka ≈ 0,02 za čelične vijke, d₂ - srednji promjer navoja (cm), D_sr - srednji promjer površine glave = 0,5∙(D_v + D_s).

Proračunavanje vijaka

Sile koje djeluju na vijke i koje stvaraju u njima naprezanja mogu biti privremene, trajne i izvanredne. Na primjer sila je na ključu kojom se priteže matica privremena jer prestane kad se matica pritegne. Trajna sila je na primjer sila tlaka vodene pare koja protječe kroz cjevovod, a djeluje na vijke, što spajanja na prirubnicama niz cijevi u jednu cjelinu. To je trajna ili radna sila, jer djeluje na vijke kada para struji kroz cjevovod. Izvanredne sile su takve, koje se javljaju katkada iznenada, na primjer od udara ili trenutnih vibracija kao posljedice neispravne montaže, ili su rezultat visokih temperatura. Sve navedene sile stvaraju u vijcima privremena ili trajna naprezanja, kojih je poznavanje važno za proračunavanje vijaka. S obzirom na međusobni odnos tih sila i naprezanja, vijci se dijele u 4 osnovne skupine, od kojih svaka ima svoje značajke, a prema tome i svoj način proračunavanja.

Vijci opterećeni na vlak

Podrobniji članak o temi: Očni vijak

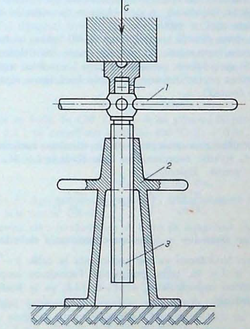
Vijci opterećeni na vlak (I. skupina) uvijaju se u neopterećenom stanju, odnosno matice se navrću neopterećene. Primjer takvog slučaja može biti vijak s okom (očni vijak) za dizanje tereta. Vijak se uvije ručnom silom i ne pritegne se snažno, pa su zato unutarnje sile i naprezanja u vijku vrlo male, te se mogu zanemariti. Kada se oko optereti obješenim teretom G, koji djeluje kao trajna vanjska sila, onda će vijak biti izložen uzdužnoj sili F. Ta će sila izazvati u njegovoj jezgri naprezanje na vlak:

$\sigma _{v}={\frac {F}{A_{1}}}={\frac {F}{\frac {\pi \cdot d_{1}^{2}}{4}}}$

gdje je: F = G, d₁ - unutarnji promjer navoja, odnosno zavojnice, koji treba odrediti iz tog izraza. Međutim, najprije kod proračuna svih vijaka treba izabrati materijal vijka, a prema materijalu uzeti iz tablica odgovarajuće dopušteno naprezanje. U tom slučaju dopušteno naprezanje σ'_{v dop} treba pomnožiti s korekcijskim faktorom ξ₁ < 1 koji obuhvaća koncentraciju naprezanja u jezgri i netočnosti kod izrade zavojnice. Obično je ξ₁ = 0,7 - 0,9, a prema tome je stvarno dopušteno naprezanje:

$\sigma _{v\,dop}=\xi _{1}\cdot \sigma _{v\,dop}'$

Onda se za proračun vijaka opterećenih jedino vlačnom silom F, uzima izraz:

$A_{1}={\frac {F}{\sigma _{v\,dop}}}$

pa se iz površine jezgre A₁ nađe u tablici odgovarajući standardni promjer za izabrani oblik zavojnice. Poslije toga preporučljivo je provjeriti površinski tlak na navojima p. On se izračunava iz:

$p={\frac {0,5\cdot F}{d_{2}\cdot H}}$

gdje je: d₂ - srednji promjer zavojnice, H - visina matice ili, kad nema matice visina takozvane "zamišljene matice". Taj stvarni površinski tlak mora biti u dozvoljenim granicama, to jest p ≦ p_dop, gdje se vrijednosti p_dop uzimaju iz tablica u priručnicima.

Za provjeru (kontrolu) površinskog tlaka može poslužiti i opći izraz:

$p={\frac {F}{z\cdot \pi \cdot d_{2}\cdot b}}\leq p_{dop}$

gdje je: z - broj aktivnih zavoja, b - korisna širina zavojnice.

Vijci opterećeni na vlak, odnosno tlak i na uvijanje određenom silom

Vijci opterećeni na vlak, odnosno tlak i na uvijanje (torziju) određenom silom (II. skupina) uvijaju se pod stanovitim opterećenjem, odnosno matice se pritežu pod opterećenjem. Kao primjer takvog slučaja može poslužiti vijak ručne dizalice. Uzdužna sila F koja se stvara u vijku kod dizanja tereta G, jest točno određena privremena vanjska sila, to jest F = G. Ona uzrokuje u jezgri vijka naprezanje na tlak:

$\sigma _{p}={\frac {F}{A_{1}}}={\frac {F}{\frac {\pi \cdot d_{1}^{2}}{4}}}$

i naprezanje zbog uvijanja zbog trenja i zbog djelovanja torzijskog momenta:

$\tau _{t}={\frac {M_{t}}{W_{p}}}={\frac {F\cdot d_{2}\cdot \tan(\phi +\rho )}{2\cdot {\frac {\pi \cdot d_{1}^{3}}{16}}}}$

gdje je: d₁ - unutarnji promjer navoja, d₂ - srednji promjer navoja, W_p = d₁³/16 polarni moment otpora presjeka jezgre vijka i M_t - moment uvijanja (torzije). Ta dva naprezanja treba složiti u jedno zamišljeno (imaginarno) naprezanje, prema izrazu nauke o čvrstoći:

$\sigma _{i}={\frac {1}{3}}\cdot \sigma +{\frac {2}{3}}\cdot {\sqrt {\sigma ^{2}+4\cdot (\alpha \cdot \tau _{t})^{2}}}$

gdje je: koeficijent popravka

$\alpha ={\frac {\sigma _{v}}{1,3\cdot \tau _{t}}},$

dok za σ treba staviti σ_p, odnosno σ_v. Taj izraz nije prikladan za neposredno proračunavanje potrebnog promjera vijka d. Pretvorbom (transformacijom) izraza s obzirom na trapeznu zavojnicu koja se najčešće upotrebljava za te vijke, može se pokazati, da je za praksu posve dovoljno računati takve vijke samo s obzirom na uzdužnu silu, odnosno s obzirom na normalno naprezanje. Uvijanje se izračunava na taj način, što se vrijednost dopuštenog naprezanja σ_dop smanjuje množenjem s dva faktora, i to s ξ₁, faktorom popravka u pogledu izrade, i ξ₂, faktorom popravka s obzirom na zamjenu zamišljenog naprezanja σ_i ekvivalentnim (jednakovrijednim) normalnim naprezanjem. Kako je srednja vrijednost ξ₁∙ξ₂ ≈ 0,75, to praktičan izraz za proračun glasi:

$A_{1}={\frac {F}{0,75\cdot \sigma _{v\,dop}}}$

gdje je:

$A_{1}={\frac {\pi \cdot d_{1}^{2}}{4}}$

površina presjeka jezgre vijka. Kako je na taj način određen promjer navoja odnosno vijka, to je preporučljivo provjeriti iznos stvarnog naprezanja s pomoću navedenog izraza za σ_i. Međutim, najvažnije je u tom drugom slučaju provjeriti (kontrolirati) površinski tlak jer je navoj vrlo opterećen, pogotovo kod vijaka u stalnom pokretu. Provjerava se s pomoću izraza:

$p={\frac {F}{z\cdot \pi \cdot d_{2}\cdot b}}\leq p_{dop}$

koji je već naveden na kraju proračuna vijaka opterećenih samo na vlak, dok se vrijednost p_dop, s obzirom na materijal vijka i matice, mogu naći u tablicama.

Kad je visina dizanja tereta velika, to dugačko vijčano vreteno, opterećeno na tlak, može biti izloženo još i izvijanju. Stoga u takvim slučajevima treba provjeriti sigurnost vijčanog vretena protiv izvijanja s pomoću koeficijenta sigurnosti S:

$S={\frac {\sigma _{k}}{\sigma _{p}}}$

gdje je: σ_k - kritično naprezanje na izvijanje određeno koeficijentom vitkosti λ, σ_p - stvarno naprezanje na tlak. Kada je λ > 96, taj je koeficijent (prema Euleru):

$S={\frac {\pi ^{2}\cdot E}{\lambda ^{2}\cdot \sigma _{p}}}$

jer je:

$\sigma _{k}={\frac {\pi ^{2}\cdot E}{\lambda ^{2}}}$

gdje je: vitkost štapa λ

$\lambda ={\frac {l}{i}}$

i - polumjer inercije, l - slobodna duljina izvijanja. Vrijednosti su tog koeficijenta za čelik od 3 do 6. Za slučaj kada je λ < 96, treba primijeniti Tetmajerov iskustveni (empirijski) izraz za kritično naprezanje σ_k = 31 - 0,114∙λ, pa je koeficijent sigurnosti jednak:

$S={\frac {31-0,114\cdot \lambda }{\sigma _{p}}}$

čije vrijednosti iznose od 1,8 do 4. Takvu provjeru treba provjeriti u svim slučajevima, kada su dugački vijci, odnosno vijčana vretene opterećeni na tlak, na primjer kod zapornih ventila, i to bez obzira na bilo koje drugo djelujuće opterećenje.

Vijci opterećeni na vlak i na uvijanje proizvoljno velikom uzdužnom silom

Vijci opterećeni na vlak i na uvijanje proizvoljno velikom uzdužnom silom (III. skupina), isto kao vijci II. skupine, također se uvijaju pod opterećenjem, ali, u tom slučaju uzdužna sila nije određene veličine, već je proizvoljno velika. Takvi se vijci nalaze primjerice kod vijčanih spojeva cilindra kompresora sa svojim poklopcem, kod spojeva cijevi (u kojima struji fluid pod tlakom) s pomoću prirubnica, ili kod spoja autoklava sa svojim poklopcem. Nepropusnost spoja osiguravaju umetnuti brtveni prsteni, rjeđe od metala (na primjer bakar), češće od klingerita. Vijci moraju biti toliko zategnuti prethodnom uzdužnom silom da bi nepropusnost spoja bila osigurana i za slučaj, kada u cilindru, odnosno u autoklavu ili cijevi, unutarnji tlak medija naraste do svog maksimuma. Ta sila, zvana prethodna zatezna sila, ostvaruje se moment (matičnim) ključem.

Moment sile na ključu M_t treba svladati moment otpora u navojima M_t1, i moment otpora trenja između matice i podloge M_t2, što znači da je:

$M_{t}=M_{t1}+M_{t2}$

Tu je:

$M_{t1}=F_{0}\cdot {\frac {d_{2}}{2}}\cdot \tan(\phi +\rho _{1})$

gdje je: F_o - prethodna zatezna sila u vijku, d₂ - srednji promjer navoja, φ - kut uspona navoja, ρ₁ - kut trenja zavojnice.

Pretvorbom tog izraza u odnosu na vijke srednjih promjera, uz prosječnu vrijednost φ + ρ₁ = 10°, dobije se:

$M_{t1}\approx 0,1\cdot F_{0}\cdot d_{1}$

Moment otpora trenja ispod matice ne utječe na naprezanje u vijku, ni na predzatezanje, te iznosi:

$M_{t2}=F_{0}\cdot a\cdot \tan \rho _{2}=\mu _{2}\cdot F_{0}\cdot a$

gdje je: F_o - prethodna zatezna sila u vijku, a - udaljenost od središnjice vijka do sredine dodirne površine matice i podloge (tan ρ₂ = μ₂) koeficijent trenja između matice i podloge. Kako je srednja vrijednost μ₂ ≈ 0,1, a krak momenta a ≈ d₁, gornji izraz prelazi u:

$M_{t2}=0,1\cdot F_{0}\cdot d_{1}$

gdje je: d₁ - promjer jezgre vijka. Onda je moment sile na ključu:

$M_{t}=M_{t1}+M_{t2}=F_{k}\cdot L=0,1\cdot F_{0}\cdot d_{1}+0,1\cdot F_{0}\cdot d_{1}=0,2\cdot F_{0}\cdot d_{1}$

gdje je: F_k - ručna sila na ključu, L - duljina ključa. Odatle je prethodna zatezna sila u vijku:

$F_{0}={\frac {5\cdot F_{k}\cdot L}{d_{1}}}$

Utjecaj vanjskih sila koje djeluju u radu, na prednapregnutu vezu vijcima III. skupine

Stegnuti dijelovi u takvim slučajevima mogu se općenito nazvati pločama. Kod pritezanja matice javlja se u vijku unutarnja sila F koja ga razvlači i produljuje, dok obje ploče istovremeno stiska i time skraćuje njihovu debljinu. Kod toga naprezanja ne smiju preći granicu elastičnosti a ni proporcionalnosti, to jest σ_v < σ_p. Tako će između prednaprezanja i produljenja, odnosno skraćenja, vrijediti Hookeov zakon. Kad se matica pritegne ključem, ostat će u vijku prethodno zatezanje (prednapregnutost) F_o koje rasteže vijak na iznos λ₁. Dakle:

$F_{0}=C_{1}\cdot \lambda _{1}$

Istovremeno na ploče djeluje to isto prethodno zatezanje F_o koje stišće ploče za λ₂. Dakle:

$F_{0}=C_{2}\cdot \lambda _{2}$

gdje su: C₁, C₂ - konstante materijala, koje pokazuju njihovu krutost. Krutost ili jedinična sila je sila koja rasteže ili skraćuje neki dio za jedinicu duljine.

Kada počne djelovati još i vanjska sila u radu F_t, dijagram će se promijeniti. Radna sila F_t povećat će zatezanje u vijku i onće se zbog toga naknadno rastegnuti za Δλ, tako da će ukupno produljenje biti λ₁ + Δλ. Po Hookeovom zakonu proporcionalnosti tom ukupnom produljenju odgovara sila F₁. Za istu duljinu Δλ promijenit će se i ploče, tako da će konačno skraćenje ploča iznositi λ₂ - Δλ. To skraćenje, po istom zakonu proporcionalnosti, može prouzročiti samo neka sila F₂. Prethodna unutarnja sila F_o promijenit će se i u vijku i u pločama od trenutka kada vijčani spoj postane izložen vanjskoj radnoj sili F_t, i to tako da će se sila rastezanja u vijku povećati od F_o do F₁, dok će se sila u pločama smanjiti od F_o na F₂. Iz toga slijedi, da i vijak i ploče sudjeluju u preuzimanju vanjske radne sile F_t proporcinalno svojim jediničnim silama, ali tako da se u novom stanju ravnoteže F₁ ≄ F₂ i iz dijagrama vidi da je F_t = F₁ - F₂.

Prema svemu tomu izlazi da stvarna sila rastezanja kojoj je izložen vijak i koja je mjerodavna za njegov proračun, nije jednaka zbroju prethodnog zatezanja F₀ i vanjske radne sile F_t, već nekoj drugoj sili F₁ < F₀ + F_t, koja se može odrediti s pomoću dijagrama, ako su poznati λ₁, λ₂ i F₀. Stvarno pritezanje vijka u radu treba da bude toliko jače, koliko su dijelovi, nazvani pločama, ili postavljene brtve elastičnije. Uvjet za predzatezanje je taj, da se ploče pod utjecajem vanjske radne sile F_t ne odvoje jedna od druge, jer bi time nepropusnost spoja bila izgubljena. Na osnovu iskustva, praktična vrijednost sile predzatezanja iznosi:

$F_{0}=(2-3)\cdot F_{t}$

i zato vijci, pritegnuti pod opterećenjem te izloženi u radu proizvoljno jakoj uzdužnoj sili, ne smiju se proračunavati samo prema vanjskoj radnoj sili F_t, a ni prema bilo kakvoj sili predzatezanja F₀, već prema gore navedenoj sili F₀ ≈ 2,5∙F_t.

Vijci čije se matice snažno pritežu, često su izloženi, ma i neznatnom, iskrivljenju izvanrednim silama koje nastaju zbog neparalelnosti podloge matice i glave, što uzrokuje u njihovom struku dodatna, ponekad vrlo velika i zato štetna naprezanja na savijanje. Takve izvanredne sile treba izbjegavati pažljivom montažom vijaka u spoju. U prednapregnutim spojevima mogu se javiti izvanredne sile i zbog toplinskog istezanja (dilatacija), koje uzrokuju sekundarna dodatna naprezanja kako u vijcima tako i u pločama. Kod viših temperatura ta naprezanja mogu biti znatna i zato nepoželjna, pa u proračunavanje vijaka treba tada uvrštavati manja dozvoljena naprezanja ili birati materijale postojane na visokim temperaturama.

Prema raspodjeli vijaka, u III. skupinu spadaju vijci izloženi istovremenom vlaku (rastezanju) i uvijanju (torziji), i u kojima uzdužna sila može imati proizvoljno veliku vrijednost. Uzdužna sila od predzatezanja povećava se u spoju, kada na njega počne djelovati još i vanjska radna sila. Određivanje te ukupne sile koja djeluje na vijak za vrijeme rada, nije jednostavno niti je uvijek moguće. Iz tih se razloga vijci te vrste računaju u praksi prema vanjskoj radnoj sili F, a dozvoljena naprezanja σ_{v dop} uzimaju iz dijagrama (iz priručnika). Taj dijagram vrijedi za spojne vijke na cijevnim vodovima, kroz koje protječe voda pod tlakom, ali uz množenje s nekim popravnim faktorom manjim od 1; dijagram vrijedi i za vijke na stapnim strojevima, na primjer na cilindru kompresora. Prema tome dopušteno naprezanje σv’dop u vijcima bit će:

$\sigma '_{v\,dop}=\xi _{3}\cdot \sigma _{v\,dop'}$

gdje za vodu do 120 °C je ξ₃ = 1, za plinove ili paru do 300 °C je ξ₃ = 0,8 i za pregrijanu paru do 400 °C je ξ₃ = 0,64.

Potreban unutarnji promjer vijka može se odrediti i neposredno prema iskustvenoj jednadžbi:

$d_{1}=\xi _{4}\cdot {\sqrt {F_{r}}}+0,5\,({\mbox{cm}})$

gdje je: F_r (kp) - vanjska radna sila, ξ₄ - faktor kvalitete izrade zavojnice, koji iznosi od 0,4 do 0,5.

Prema tako izračunatom d₁ treba iz dijagrama naći odgovarajuće dozvoljeno naprezanje i provjeriti ga s pomoću izraza:

$\sigma _{v}={\frac {F_{r}}{A_{1}}}={\frac {F_{r}}{\frac {\pi \cdot d_{1}^{2}}{4}}}$

Vijci izloženi djelovanju poprečnih sila

Poprečne sile mogu ponekad prouzrokovati u vijku naprezanje na vlak, na savijanje i na smicanje (odrez). Postoje 3 načina za poništenje poprečnih sila, za čije preuzimanje vijak kao konstruktivni dio nije inače pogodan.

Prvi način

Vijak se stavi u rupu promjera do koji je nešto veći od promjera vijka d. Ploče ili limovi stegnu se maticom toliko snažno, da se stvori otpor protiv klizanja limova, koji drži ravnotežu poprečnoj sili F_s. U tom slučaju vijak će biti izložen uzdužnoj vlačnoj sili F stvorenoj pritezanjem matice, koja se može naći iz uvjeta da je μ∙F ≥ F_s, to jest:

$F={\frac {F_{s}}{\mu }}$

gdje je koeficijent kliznog otpora μ = 0,1 - 0,2. Prema tome vlačno naprezanje u njegovoj jezgri iznosi:

$\sigma _{v}={\frac {F}{\frac {\pi \cdot d_{1}^{2}}{4}}}$

a potreban presjek jezgre izračuna se iz izraza:

$A_{1}={\frac {F}{\sigma _{v\,dop}}}$

Takvi vijci kod kojih je d_o > d zovu se neprilagođeni vijci. Oni su upotrebljivi za poprečne sile samo kod slučajeva manje-više mirnih opterećenja. Kod promjenjivih opterećenja ili vibracija smanjila bi se uzdužna sila u vijku zbog popuštanja matice, pa bi vijak bio izložen smicanju i savijanju. Zato za preuzimanje poprečnih sila kod promjenjivih opterećenja služe takozvani prilagođeni vijci.

Drugi način

Drugi način sastoji se u spajanju ploča ili limova tim prilagođenim vijcima, kod kojih je promjer struka vijka d, jednak promjeru rupe d_o. Prema tome između vijka i ploča nema nikakve zračnosti, tako da struk vijka pristaje uz provrt. U tom slučaju struk vijka opterećen poprečnim silama F_s na smicanje, pa je naprezanje smika jednako:

$\tau _{s}={\frac {F_{s}}{\frac {\pi \cdot d_{s}^{2}}{4}}}$

Prema tome prilagođeni se vijci proračunavaju na smicanje, jer tu struk igra glavnu ulogu, a navoj vijka sporednu jer matica u tom slučaju nije jako pritegnuta. Potrebna površina presjeka struka prilagođenih vijaka:

$A={\frac {\pi \cdot d_{s}^{2}}{4}}$

određuje se iz izraza:

$A={\frac {F_{s}}{z\cdot \tau _{s\,dop}}}$

gdje je: F_s - poprečna sila koja otpada na jedan vijak, z - broj presjeka izloženih smicanju, τ_{s dop} - dopušteno naprezanje na smik. Odatle se dobije potreban promjer struka:

$d_{s}={\sqrt {\frac {4\cdot A}{\pi }}}$

ds = korj. 4∙A / π

Poslije toga mora se provjeriti površinski tlak između struka vijka i stijenki provrta prema izrazu:

$p={\frac {F_{s}}{d_{s}\cdot b}}\leq p_{dop}$

gdje je: F_s - poprečna sila u jednom smjeru, koja djeluje na ukupnu debljinu b spojenih dijelova. Ako su dvije spojene ploče različitih debljina, u račun treba uvrstiti manju debljinu.

Treći način

Najteže i najnepovoljnije je za vijak istovremeno opterećenje poprečnim i uzdužnim silama. Taj se način sastoji u rasterećenju vijka od poprečnih sila, odnosno u njihovom onemogućavanju da na njega djeluju. To se postiže konstruktivnim rješenjima i mjerama. Na primjer može se postaviti umetnuti cilindrični prsten oko struka vijka, ili okrugli zatik, ili stepenastu izbočinu. U takvim slučajevima vijci preuzimaju na sebe jedino uzdužnu silu u spoju, prema kojoj se oni i proračunavaju prema prikazanom načinu. Dijelovi koji preuzimaju poprečne sile (prsten, zatik i tako dalje) treba proračunavati na smicanje i provjeriti površinski tlak na njihovim dosjednim površinama.