Oduzimanje
Oduzimanje je jedna od četiri osnovnih aritmetičkih operacija. Oduzimanje je suprotno od zbrajanja, što znači ako broju, recimo x, dodamo y i od dobivenog broja oduzmemo y ponovno ćemo dobiti x. Oduzimanje označujemo znakom minusa u infiksnoj notaciji.
Za oduzimanje ne vrijedi komutativnost, već antikomutativnost, pa dajemo imena članovima. Uobičajna imena su umanjenik, umanjitelj i razlika. U jednadžbi a - b = c, a je umanjenik, b umanjitelj, a c razlika.
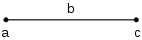
Zamislimo dužinu duljine b gdje je lijevi kraj označen sa slovom a, a desni kraj slovom c. Počevši od a, potrebno je b koraka udesno da dođemo do c. Ovakva kretnja se može matematički opisati zbrajanja:
a + b = c
Od c je potrebno b koraka ulijevo da se vratimo do a. Ovakva kretnja se može matematički opisati oduzimanjem:
c - b = a

Sad zamislimo dužinu označenu s brojevima 1, 2 i 3. Od položaja 3 nisu potrebni koraci ulijevo da se ostane na 3, dakle 3 - 0 = 3. Potrebna su dva koraka ulijevo da se dođe do položaja 1, dakle 3 - 2 = 1. Slika je neodgovarajuća da se prikaže što bi se dogodilo nakon 3 koraka ulijevo. Da bi se to prikazalo potrebno je produžiti dužinu.
Za oduzimanje prirodnih brojeva potrebno je početi s polupravcem koji sadrži sve prirodne brojeve(0,1,2,3,4,5, ...). Od 3, potrebno je napraviti 3 koraka ulijevo da se dođe na 0, dakle 3 - 3 = 0. Ali, 3 - 4 nije moguće prikazati jer prelazi polupravac.
Rješenje je pravac s cijelim brojevima(..., -3, -2, -1,0,1, 2, 3, ...). Od 3, potrebno je 4 koraka ulijevo da se dođe do -1:
3 - 4 = -1
Postoje slučajevi gdje oduzimanje kao zasebna operacija postaje problematična. Primjerice, 3 - (-2) (oduzimanje -2 od 3) nije odmah očito na brojevnom pravcu jer nam nije odmah jasno što znači pomaknuti se -2 koraka ulijevo. Jedno rješenje je prikazati oduzimanje kao zbrajanje. Dodatan znak minusa označuje inverziju zbrajanja. Tada imamo 3 - (-2) = 3 + 2 = 5.
- Browell, W. A. (1939). Learning as reorganization: An experimental study in third-grade arithmetic, Duke University Press. (engl.)
- Subtraction in the United States: An Historical Perspective, Susan Ross, Mary Pratt-Cotter, The Mathematics Educator, Vol. 8, No. 1 (original publication) and Vol. 10, No. 1 (reprint.) http://math.coe.uga.edu/TME/Issues/v10n2/5ross.pdf Arhivirana inačica izvorne stranice od 11. kolovoza 2017. (Wayback Machine) (engl.)
