Stirlingov ciklus
Stirlingov ciklus ili proces je termodinamički kružni ciklus po kojem rade Stirlingovi uređaji. Ciklus i uređaj koji radi po njemu su osmislili i patentirali braća Robert Stirling, svećenik, i James Stirling, inženjer, 1816. godine. Kako je riječ o termodinamičkom kružnom ciklusu, to znači da se ciklus vodi između dva toplinska spremnika različitih temperatura, tj. između ogrjevnog i rashladnog spremnika, a ukupna izmijenjena toplina između toplinskih spremnika jednaka je ukupnom izvršenom mehaničkom radu. Stirlingov ciklus može biti desnokretan ili lijevokretan; ako je desnokretan, mehanički rad se dobiva te uređaj radi kao motor, a ako je lijevokretan, mehanički rad se troši te uređaj radi kao rashladni uređaj ili dizalica topline. Specifičnost Stirlingovog ciklusa u odnosu na ostale kružne procese je taj što osim što je teoretski izveden kao zatvoren sustav, tako je izveden i u tehničkoj praksi; to znači da uređaji koji rade na principu Stirlingovog ciklusa nemaju usis i ispuh i da je unutar sustava sadržana konstantna masa radne tvari. Ciklus se u osnovi sastoji od dvije izoterme i dvije izohore.

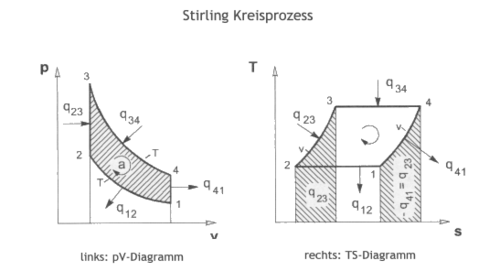
Teorijski Stirlingov ciklus razmotrit će se kao desnokretni zatvoreni ciklus; ciklus se sastoji od četiri promjene stanja:
- 1-2: izotermna kompresija - rashladni spremnik odvodi toplinu radnom mediju zbog čega se radnom mediju smanjuje volumen
- 2-3: izohorno dovođenje topline - stlačeni radni medij prolazi kroz regenerator koji ga grije dovodeći mu toplinu pri konstantnom volumenu
- 3-4: izotermna ekspanzija - ogrjevni spremnik dovodi toplinu radnom mediju povećavajući mu volumen
- 4-1: izohorno odvođenje topline - radni medij se vraća kroz regenerator predajući mu toplinu pri konstantnom volumenu.
Dok se na jednom dijelu cilindra izvode promjene stanja 2-3 i 3-4, na drugom dijelu cilindra se izvode promjene stanja 4-1 i 1-2 i obratno.
Specifična toplina se dovodi pri promjenama stanja 2-3 i 3-4:
gdje je - specifična toplina, - specifični toplinski kapacitet pri konstantnom volumenu, - termodinamička temperatura, - specifična entropija, - individualna plinska konstanta, - specifični volumen. Ukupno dovedena specifična toplina iznosi:
- .
Specifična toplina se odvodi pri promjenama stanja 4-1 i 1-2:
- .
Ukupno odvedena specifična toplina iznosi:
- .
Kako je ukupno dobiveni specifični rad jednak ukupno izmijenjenoj specifičnoj toplini:
- ,
iz toga slijedi:
- .
U gornjoj jednadžbi su zamijenjena mjesta temperaturama i te specifičnim volumenima i jer se predznakom - uz veličinu već naglasila činjenica da se radi o odvedenoj toplini. Kako se proces izvodi regenerativno, izohorno dovedena i izohorno odvedena specifična toplina su teorijski jednake, ali suprotnih predznaka tako da se one poništavaju. Još se može primijetiti da su i iz čega se zaključuje da su te iz tih spoznaja slijedi:
Gornja relacija predstavlja ukupno dobiveni specifični rad ciklusa, a ako ga se pomnoži s ukupnom masom radnog medija, tada se dobije ukupno dobiveni rad desnokretnog zatvorenog teorijskog Stirlingovog ciklusa. Snaga stroja koji bi radio na principu teorijskog Stirlingovog ciklusa glasi:
gdje je - ukupna masa radnog medija, a - broj okretaja stroja u sekundi.
Termički stupanj djelovanja Stirlingovog ciklusa se definira kao:
- ,
a kako je u teorijskom ciklusu regenerator idealan ( ), tada vrijedi:
- .
Konačno,termički stupanj djelovanja teorijskog Stirlingovog ciklusa glasi:
- .
Teorijski Stirlingov ciklus s idealnim regeneratorom prema termičkom stupnju djelovanja potpuno je ekvivalentan termičkom stupnju djelovanja Carnotovog (najveći termički stupanj djelovanja) i Ericssonovog ciklusa (Ericssonov ciklus postiže Carnotov termički stupanj djelovanja samo uz idealni regenerator kao i Stirlingov ciklus), a veći od termičkog stupnja djelovanja Jouleovog, Dieselova i Ottova ciklusa. Prema dobivenom radu, najbolji ciklus je Ericssonov, a zatim slijede Stirlingov, Jouleov, Dieselov, Ottov te Carnotov ciklus.
Nijedan današnji stroj ne radi na principu teorijskog kružnog ciklusa pa tako ni na principu teorijskog Stirlingovog ciklusa; razlozi su sljedeći: loše brtvljenje, postojanje volumena štetnog prostora, trenje, regeneratori koji nisu idealni... Unatoč tomu, možemo približno opisati tok Stirlingovog ciklusa uzimajući u obzir određene nesavršenosti te se tako dobije realni Stirlingov ciklus.
Stirlingov motor [2]
Stirling cycle [3]
Stirling-Kreisprozess [4]
- ↑ Kolin, Ivo, Stirling motor, 1991., Zagreb University Publications, Ltd.
- ↑ Galović, Antun, Termodinamika I, Fakultet strojarstva i brodogradnje, Zagreb, 2008., ISBN 953-6313-44-8
- ↑ [1][neaktivna poveznica] Laboratorij za termoenergetiko

![{\displaystyle q_{23}=c_{v}\Delta T_{23}\ =c_{v}\left(T_{3}-T_{2}\right)\ >0\quad \left[J/kg\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74e9d46aa8134a86f618c05a1910266b715b68c7)
![{\displaystyle q_{34}=T_{max}\Delta s_{34}\ =T_{max}R\ ln\left({\frac {v_{4}}{v_{3}}}\right)\ >0\quad \left[J/kg\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a60428e9d98f28e8be367ed44bed5e5cb5d9b3ee)






![{\displaystyle q_{dov}=q_{23}+q_{34}\ >0\quad \left[J/kg\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79bfae485c687d84ac1134d1673106ff6f8eb1dc)
![{\displaystyle q_{41}=c_{v}\Delta T_{41}\ =c_{v}\left(T_{1}-T_{4}\right)\ <0\quad \left[J/kg\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/800ff35803d3bc2db0261589a6b0e775db1720e6)
![{\displaystyle q_{12}=T_{min}\Delta s_{12}\ =T_{min}R\ ln\left({\frac {v_{2}}{v_{1}}}\right)\ <0\quad \left[J/kg\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25be99584ad543ae9c96b3f673888da1c8856e79)
![{\displaystyle q_{odv}=q_{41}+q_{12}\ <0\quad \left[J/kg\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39175d6a3b86041cbf94b8f90de665d61f0169a8)



![{\displaystyle w_{uk}=c_{v}\left(T_{3}-T_{2}\right)+T_{max}R\ ln\left({\frac {v_{4}}{v_{3}}}\right)-\left[T_{min}R\ ln\left({\frac {v_{1}}{v_{2}}}\right)+c_{v}\left(T_{4}-T_{1}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be4a9d39f22a9bfbff0f64879b1cb90630d275f2)









![{\displaystyle w_{uk}=\left(T_{max}-T_{min}\right)R\ ln\left({\frac {v_{4}}{v_{3}}}\right)\ >0\quad \left[J/kg\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3b84451d43af4d5e0dd33e7d820bfb0a2830e5e)

![{\displaystyle P_{S}=w_{uk}m_{uku}n\ >0\quad \left[W\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/706f692265a9a6a4121b3997024de79badb1d2fc)





