Singularna točka

Šiljak i čvorna točka česte su kod algebarskih krivulja.

Singularna točka (lat. singularis: jedini) u diferencijalnoj geometriji, točka u kojoj vrijednost funkcije postaje beskonačna, višeznačna i nedefinirana ili njezin graf gubi uobičajena svojstva.

Singularne točke ne smiju se zamijeniti za neke druge bitne točke u matematičkoj analizi kao što su lokalni ili globalni minimum i maksimum, sedlasta točka, točka prijevoja ili pregiba (inflekcijska točka) i sl.

Vrste singularnih točaka

Postoji više načina na koje krivulja može biti deformirana, pa time postoje sljedeći tipovi izoliranih točaka:

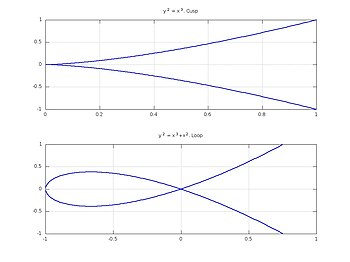
• čvorna točka u kojoj krivulja samu sebe presijeca;
• izolirana točka koja zadovoljava jednadžbu krivulje, ali ne leži na njoj,
• šiljak (ili povratna točka) u kojoj se smjer krivulje mijenja (u suprotni); točka samotangiranja u kojoj krivulja dodiruje samu sebe,
• točka loma u kojoj krivulja "skokovito" mijenja smjer, ali za razliku od šiljka ima različite tangente na oba dijela prekida krivulje,
• točka prekida u kojoj se krivulja prekida,
• asimptotska točka oko koje se krivulja ovija beskonačno mnogo puta, približavajući joj se na po volji malu udaljenost. Kod analitičkih funkcija kompleksne varijable to je točka u kojoj funkcija nije derivabilna (singularitet).