Snelliusov zakon
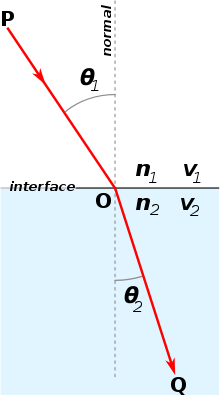


Snelliusov zakon ili Snellov zakon (prema Willebrordu Snelliusu) se odnosi na dobro poznatu pojavu lomljenja svjetlosti (refrakcije) na granici dvaju sredstava, a glasi: "Svjetlost koja pada na granicu dvaju sredstava indeksa loma n1 i n2 prijelazom iz jednog u drugo sredstvo lomi se tako da:
- upadna zraka, okomica na granicu sredstava i lomljena zraka leže u istoj ravnini,
- kut loma i kut upada zadovoljavaju takozvani Snelliusov zakon:
ili
pri čemu su: θ1 – kut upadne zrake svjetlosti, θ2 – kut loma, v1 i v2 brzine vala, a n1 i n2 odgovarajući indeksi loma sredstva iz kojega zrake dolaze i sredstva u koje ulaze."[1]
Indeks loma u nekom sredstvu je omjer brzine svjetlosti u vakuumu (najveća moguća brzina) i brzine svjetlosti u tom sredstvu. Optički gušće sredstvo je ono koje ima veći apsolutni indeks loma, a ono čiji je indeks loma manji zove se optički rjeđe sredstvo. Iz iskustva znamo da će ravan štap gurnut u vodu izgledati prelomljen, to je posljedica loma svjetlosti.
Indeks loma (oznaka n) je bezdimenzionalna fizikalna veličina koja opisuje međudjelovanje svjetlosti i optički prozirne tvari, a definirana je kao omjer brzine svjetlosti u vakuumu c i brzine svjetlosti u tvari v,
Posljedica je promjene brzine svjetlosti promjena pravca njezina širenja pri prelasku iz jednoga optičkog sredstva u drugo. Što je indeks loma veći, veća je promjena pravca, odnosno veći je lom svjetlosti (refrakcija). Indeks loma može se s pomoću Snelliusova zakona odrediti iz geometrijskih odnosa kutova zraka svjetlosti prema površini sredstva u kojem dolazi do loma:
gdje je: θ1 – upadni kut prema okomici na površinu sredstva, θ1 – kut loma, n1 – indeks loma optičkoga sredstva iz kojega svjetlost dolazi, a n2 – indeks loma optičkoga sredstva u koje svjetlost ulazi. Često se rabi relativni indeks loma, koji je jednak omjeru indeksa loma dvaju sredstava:
Svjetlost se u nekoj tvari širi brzinom:
gdje je: εr – relativna dielektrična permitivnost tvari, a μr – relativna magnetska permeabilnost. Kako za relativnu magnetsku permeabilnost u optički prozirnom sredstvu vrijedi μr ≈ 1, proizlazi da indeks loma ovisi samo o relativnoj dielektričnoj permitivnosti:
Međutim, za mnoge tvari dolazi do odstupanja od toga izraza, zbog postojanja električnih dipola u dielektricima i ovisnosti relativne dielektrične permitivnosti o frekvenciji svjetlosti.[2]







