Tuneliranje

Budući da polumjer atomske jezgre iznosi oko 10^-15 m, a brzina alfa-čestice koja se u njemu kreće iznosi oko 10⁶ m/s, izlazi da alfa-čestica dolazi do vanjske površine približno 10⁶/10^-15 = 10²¹ puta u sekundi, odnosno da ona pobjegne iz jezgre nakon 10²¹ pokušaja. To je u stvari bit tuneliranja ili tunelskog učinka.

Tuneliranjem postoji vjerojatnost da elementarna čestica svlada prepreku (potencijalnu barijeru) zahvaljujući valnim svojstvima koja kvantna mehanika pridjeljuje elementarnim česticama, valna funkcija čestice ne iščezava ni u samoj barijeri, ni iza nje.

Postoji određena vjerojatnost da se elementarna čestica nađe i u klasično zabranjenim područjima prostora. Ta vjerojatnost ovisi o visini i širini barijere, a pokusi potvrđuju da je, pri naletu mnoštva čestica, broj onih koje prođu barijeru proporcionalan kvantno-mehanički izračunanoj vjerojatnosti.

Skica pretražnog mikroskopa s tuneliranjem.

Ogib ili difrakcija elektrona je pokazala da se elektroni ponašaju i kao čestice i kao valovi (dualizam).

Prikaz valova tvari u ogibu (difrakciji) elektrona.

Refrakcija ili lom svjetlosti.

Refleksija ili odbijanje valova: zraka svjetlosti koja pada na neku ravninu reflektira se tako da je upadni kut α jednak kutu refleksije β, a upadna i reflektirana (odbijena) zraka leže u istoj ravnini.

Totalnu refleksiju često vide ronioci u moru.

Lom svjetlosti u akrilnoj planparalelnoj ploči.

Tuneliranje, tunelski efekt ili tunelski učinak je kvantnomehanička pojava pri kojoj postoji vjerojatnost da elementarna čestica svlada prepreku (potencijalnu barijeru) kada to zakoni klasične fizike ne dopuštaju. Primjerice, pri naletu čestice na središte odbojne sile kojoj je potencijalna energija veća od kinetičke energije čestice, klasično je moguće samo odbijanje čestice. Ipak, zahvaljujući valnim svojstvima koja kvantna mehanika pridjeljuje elementarnim česticama, valna funkcija čestice ne iščezava ni u samoj barijeri, ni iza nje. Stoga postoji određena vjerojatnost (dana kvadratom modula valne funkcije) da se čestica nađe i u klasično zabranjenim područjima prostora. Ta vjerojatnost ovisi o visini i širini barijere, a pokusi potvrđuju da je, pri naletu mnoštva čestica, broj onih koje prođu barijeru proporcionalan kvantno-mehanički izračunanoj vjerojatnosti.

Tuneliranjem su protumačene mnogobrojne pojave u nuklearnoj i atomskoj fizici, poput alfa raspada atomskih jezgri (George Gamow, 1928.), spontane nuklearne fisije, emisije elektrona iz metalnih površina u supravodičima. U posljednjem slučaju riječ je o posebnom tipu tuneliranja vezanom uz energijski procijep i promijenjenu gustoću stanja za normalno vodljive kvazičestice u supravodiču. Struja elektrona koji prolaze tuneliranjem kroz potencijalnu barijeru našla je primjenu u pretražnom mikroskopu s tuneliranjem, kojom se ispituje elektronska struktura površina vodljivih uzoraka.

BCS-teorija

Podrobniji članak o temi: BCS-teorija

BCS-teorija ili Bardeen-Cooper-Schriefferova teorija je prva mikroskopska teorija supravodljivosti (1957.). Polazi od pretpostavke da na vrlo niskim temperaturama u kristalnoj rešetki supravodiča privlačno međudjelovanje elektron–rešetka–elektron nadjačava odbojnu električnu silu među elektronima, tj. da elektroni pri prolasku kroz rešetku privlače njezine ione, što rezultira povećanjem gustoće pozitivnog naboja u tom području i, dok se rešetka ne vrati u ravnotežno stanje, privlači druge elektrone. U takvim uvjetima elektroni kojima su spinovi i količine gibanje suprotni gibaju se u parovima (Cooperovi parovi), a svaki par elektrona na međusobnoj udaljenosti od približno 100 nm giba se kroz kristalnu rešetku bez gubitka energije i može tunelirati kroz izolatorsku barijeru. Porastom temperature atomi rešetke sve jače titraju, iznad kritične temperature razdvajaju elektronske parove, elektroni se više ne mogu gibati bez gubitaka i pojavljuje se električni otpor. Za razvoj BCS-teorije John Bardeen, Leon Neil Cooper i John Robert Schrieffer dobili su Nobelovu nagradu za fiziku 1972.

Pretražni mikroskop s tuneliranjem

Podrobniji članak o temi: Pretražni mikroskop s tuneliranjem

Pretražni mikroskop s tuneliranjem (STM, kratica od engl. Scanning Tunneling Microscope) je mikroskop kojim se promatraju površine metala i drugih električki vodljivih materijala preciznošću na razini atoma. Najvažniji je dio pretražnog mikroskopa s tuneliranjem oštri vrh od volframa, platine, iridija, ugljikove nanocijevi ili nekog drugog vodljivoga materijala koji u idealnom slučaju čini samo jedan ili nekoliko atoma. Kada je vrh blizu površine (nanometar i manje), u vakuumu između vrha i površine dolazi do tuneliranja elektrona. Kako se vrh pomiče duž površine, zbog površinskih nepravilnosti i nehomogenosti na razini atoma, udaljenost i električna struja između vrha i površine se mijenjaju, a promjena jakosti struje može se tumačiti kao slika površine. Za otkriće pretražnog mikroskopa s tuneliranjem, Gerd Binnig i Heinrich Rohrer dobili su Nobelovu nagradu za fiziku 1986.

Tuneliranje ili tunelski učinak alfa-čestica

Velika je poteškoća nastala da se objasni kako je moguće da alfa-čestice, čija kinetička energija iznosi pri izbacivanju iz radioaktivnih atomskih jezgri od 4 do 10 MeV, da prođu kroz potencijalnu energetsku barijeru, čije najveće vrijednosti kod elemenata s velikim atomskim brojem iznose oko 25 MeV. Prema klasičnoj teoriji, izlazi da alfa-čestice, koje se nalaze u unutrašnjosti atomske jezgre, ne mogu prodrijeti kroz barijeru i iz njega se osloboditi s energijom, koja je manja od energije potencijalne barijere.

Isto tako, teško je bilo objasniti zašto radioaktivni elementi imaju tako dugo vrijeme poluraspada, koji na primjer za radij-226 iznosi 1600 godina. To znači da se u tako dugom vremenskom periodu, nukleoni (protoni i neutroni) moraju držati zajedno u atomskom jezgru, iako ponekad spontano, bez vanjskih utjecaja, dva protona i dva neutron u obliku alfa-čestice budu izbačeni iz nje.

Taj problem su teoretski riješili 1928. George Gamow, a neovisno o njemu Ronald Wilfred Gurney i Edward Condon, razvivši teoriju tuneliranja. Prema kvantnoj fizici postoji vjerojatnost da se alfa-čestica s određenom energijom, koja je manja od energije potencijalne barijere, oslobodi atomskog jezgra, kad dođe do njegove površine. Ova vjerojatnost je veća ako je veća energija alfa-čestice i ako je širina barijere manja od vrijednosti njene energije. Alfa-čestica će na neki način dobiti dovoljnu količinu energije od drugih nuklearnih čestica, za svladavanje potencijalne barijere.

Za alfa-čestice sposobne da dospiju do vanjske površine i da ponovno budu ubačene u atomsko jezgro, postoji učestalost. Vrijednost ove učestalosti može se odrediti dijeljenjem veličine polumjera atomske jezgre s procijenjenom brzinom, kojom se alfa-čestice kreću u atomskoj jezgri. Budući da polumjer atomske jezgre iznosi oko 10^-15 m, a brzina alfa-čestice koja se u njemu kreće iznosi oko 10⁶ m/s, izlazi da alfa-čestica dolazi do vanjske površine približno 10⁶/10^-15 = 10²¹ puta u sekundi, odnosno da ona pobjegne iz jezgre nakon 10²¹ pokušaja. To je u stvari bit tuneliranja.

Val materije u potencijalu, lom i refleksija

Podrobniji članak o temi: Valovi tvari

Valovi materije se uglavnom razmatraju izvan djelovanja vanjskih sila. Tog ograničenja treba da se sada riješimo. Katodne zrake nose električni naboj i, prema tome, izvrgnute su djelovanju električnih sila. Odmah se može tvrditi kakvo će biti uzajamno djelovanje između valova materije i vanjskih sila. Odlučnu riječ ipak imaju pokusi. No imajući pred očima analogiju vala i čestice, možemo općenito zaključiti kako će se mijenjati valna duljina valova materije u vanjskom električnom potencijalu.

Djelovanje električne sile opisujemo u valnoj teoriji električnim potencijalom V. Potencijal, pomožen električnim nabojem čestice e∙V, daje potencijalnu energiju U. Pri proučavanju vanjskih djelovanja služit ćemo se potencijalom ili potencijalnom energijom, što znači razliku samo u konstantnom čimbeniku e.

Kad se katodne zrake kreću u vanjskom potencijalu, mijenja se njihova brzina. Promjena brzine mora prema de Broglievom odnosu biti vezana s promjenom valne duljine. Za česticu je zbroj kinetičke i potencijalne energije konstanta:

${\frac {m\cdot v^{2}}{2}}+U=E$

Odatle izlazi kako se impuls čestice mijenja pod djelovanjem:

$m\cdot v={\sqrt {2\cdot m\cdot (E-U)}}$

Prema de Broglievom odnosu određena je impulsom valna duljina vala materije:

$\lambda ={\frac {h}{\sqrt {2\cdot m\cdot (E-U)}}}$

Iz ove jednadžbe izlazi kako se mijenja valna duljina vala materije na različitim mjestima u prostoru. Kreću li se katodne zrake nasuprot djelovanju električne sile, tada se valna duljina povećava. Kad se, naprotiv, katodne zrake kreću u smjeru električne sile, tada se valna duljina umanjuje.

U teoriji svjetlosti promjena valne duljine uzrokovana je različitom optičkom gustoćom sredstva. Te različite gustoće sredstva mjere se indeksom loma koji izražava za koliko je umanjena valna duljina svjetlosti na tom mjestu prema valnoj duljini u vakuumu. Gibanje valova materije pod djelovanjem vanjskih sila potpuno je analogno širenju svjetlosti u sredstvu s promjenjivom optičkom gustoćom. Sve učinke, koji dolaze u širenju svjetlosti u sredstvu promjenjive optičke gustoće, moramo naći i u gibanju katodnih zraka. Širenje valova materije i svjetlosti dade se opisati istim zakonima, samo što riječ svjetlost treba prevesti u riječ materija, a optička gustoća sredstva u potencijalnu energiju. Gibanju materije prema rastu potencijalne energije odgovara širenje svjetlosti prema optički gušćem sredstvu (valna duljina se umanjuje). Tako imamo za gibanje valova materije zorni model. Zakoni gibanja valova materije svedeni su na poznate zakone širenja svjetlosti. Na nekoliko jednostavnih primjera pokazat ćemo do kakvih posljedica za ponašanje materije vodi takva zorna slika.

Osnovna pojava u optici je lom i refleksija svjetlosti na granici između dva sredstva. Promotrimo prijelaz svjetlosti iz gušćeg sredstva u rjeđe, na primjer iz stakla u zrak. Kod katodnih zraka to odgovara širenju zraka prema naglom skoku potencijala. Do određene ravnine, okomite na smjer širenja, ima potencijal vrijednost nula, a iza te ravnine naglo skače na konačnu veličinu i ostaje iza te ravnine stalno na toj vrijednosti. Prema veličini potencijalnog skoka možemo razlikovati dva slučaja:

1. Skok potencijalne energije manji je od energije E, dakle je razlika E - U pozitivna i iza potencijalnog skoka. Tada je valna duljina realna ispred i iza potencijalnog skoka. Pustimo li katodne zrake da se šire prema takvom potencijalnom skoku, na mjestu potencijalnog skoka jedan se dio zraka reflektira, dok se drugi dio širi dalje u prostor više potencijalne energije. Valovi materije reflektiraju se i lome na mjestu potencijalnog skoka kao svjetlost na granici između stakla i zraka. Istodobna refleksija i lom katodnih zraka stoje u nepremostivoj suprotnosti s klasičnom mehanikom. Shvatimo li katodne zrake kao čestice (korpuskule) jedinstvene brzine, nikada se istovremeno ne može dogoditi refleksija i lom. Ako je potencijalna energija manja od sveukupne energije, po klasičnoj mehanici sve se čestice kreću dalje naprijed. Poslije toga skoka kreću se, naravno, s nešto manjom brzinom. Uistinu se, međutim, opaža i lom i refleksija katodnih zraka na granici između različitih potencijalnih energija. Istovremena refleksija i lom daju se objasniti samo valnom prirodom.

1. Skok od U veći je od energije E. U tom slučaju je razlika E - U iza potencijalnog skoka negativna, pa je duljina vala materije imaginarna. Iza potencijalnog skoka ne mogu se u tom slučaju širiti valovi materije. Imaginarna valna duljina znači u optici totalnu refleksiju. Sav val se reflektira, ništa ne ulazi u drugo sredstvo. Tu pojavu možemo na primjer promatrati pri prijelazu svjetlosti iz stakla u zrak. Ako je kut između okomice na staklo i zrake svjetlosti veći od 42°, nastupa totalna refleksija, i cjelokupna svjetlost se reflektira.

Potpunu refleksiju isto tako nalazimo u valnoj kao i u korpuskularnoj (čestica) slici materije. Čestice koje imaju manju energiju od energije potencijalnog skoka sve se vraćaju, sve se reflektiraju na potencijalnom zidu. Čestica, koja bi doprla dalje nadesno od točke gdje je U = E imala bi potencijalnu energiju, a to je besmislica. Za razliku od prvog slučaja, kod kojeg je energija elektrona bila veća od skoka potencijalne energije, u ovom drugom slučaju vodi korpuskularna i valna slika materije prema istom rezultatu.

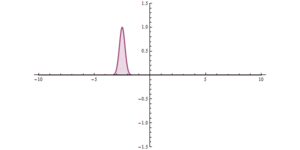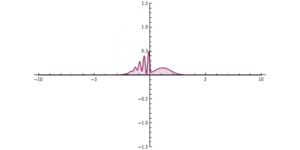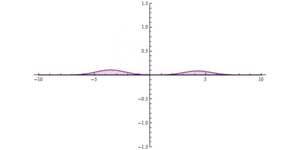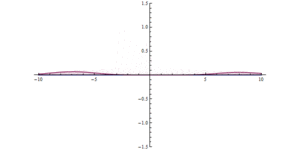
Temeljna razlika između čestica i valova u klasičnoj fizici pokazuje slika da se u valnoj teoriji može poništiti totalna refleksija. Totalna refleksija svjetlosti može se ukloniti tako da iza jedne staklene ploče postavimo u ne prevelikom razmaku drugu staklenu ploču. Tada se i u drugoj staklenoj ploči širi svjetlost, iako se u zraku između staklenih ploča ne primjećuje svjetlost. Kod valova materije toj drugoj postavljenoj ploči stakla odgovara ponovni skok potencijala prema dolje. Poslije ponovnog pada potencijala postaje potencijalna energija ponovno manja od energije. Valna duljina je opet realna, i u tom dijelu prostora ponovo se mogu širiti katodne zrake. Pustimo li katodne zrake da se šire prema takvom potencijalnom brijegu, brzina se sve više umanjuje i konačno postaje ta brzina jednaka nuli. U okolini mjesta, gdje je U = E, katodne se zrake bitnim dijelom reflektiraju. No po zakonima valnog širenja još uvijek jedan dio amplitude vala prodire i u potencijalni brijeg gdje je valna duljina imaginarna. Do mjesta x₁ u brijegu, gdje valna duljina ponovo postaje realna, umanjila se ta amplituda na izvjesnu malu, ali ipak od nule različitu vrijednost. Od mjesta x₁ nadesno ta mala amplituda ostaje konstantom i titra poput amplitude ravnog vala. Dakle, iza potencijalnog brijega širi se ponovo val materije, pojavljuju se opet katodne zrake. Te katodne zrake šire se iza potencijalnog brijega s prvobitnom brzinom, no s mnogo manjom jačinom (intenzitetom). Pojavljivanje katodnih zraka iza potencijalnog brijega samo je tada znatno ako potencijalni brijeg nije ni jako visok ni jako širok. Valovi materije prodiru otprilike za svoju valnu duljinu u brijeg potencijala.

Prodiranje materije kroz potencijalne brijegove svojstveno je za valnu teoriju, a potpuno je nespojivo s korpuskularnom slikom materije. Promatramo li katodne zrake kao čestice koje se kreću prema potencijalnom brijegu, tad se čestice zaustavljaju na mjestu gdje je njihova energija jednaka potencijalnoj. Na tom mjestu sve se čestice vraćaju prema natrag. Potpuno je isključeno da bi čestice prodrle u brijeg nakon što su se zaustavile. U brijegu bi imale imaginarnu brzinu, a to je, naravno, nestvarno. Na ovom mjestu očituje se vrlo drastično kako se iste pojave, koje su nespojive s korpuskularnom zornom teorijom materije, vrlo zorno tumače u valnoj slici materije. Taj učinak prodiranja materije kroz potencijalne brijegove nazvan je tunelefekt i od velike je važnosti za tumačenje atomskih procesa.

Budući da se val rasprostire poglavito u području gdje je energija veća od potencijalne energije, nužno su dimenzije vala materije u stabilnom stanju najmanje. Kod najniže energije atoma je na primjer to područje znatno manje negoli za prvu pobuđenu energiju. Kod te pobuđene energije promjer je vala materije otprilike 4 puta veći od promjera vala materije osnovnog stanja. U valnom modelu nailazimo na iste odnose koji vladaju i u Bohrovu modelu atoma. Točan račun pokazuje da se dimenzije rasprostiranja vala u stabilnom stanju podudaraju potpuno s iskustvenim dimenzijama atoma. Područje rasprostiranja elektronskog vala jednako je s veličinom atoma. Atom nije ništa drugo do elektronski val uhvaćen od atomske jezgre. Slaganje između kinetičkog promjera atoma i rasprostiranja vala nije slučajno, već je dano samom prirodom atoma. Elektronski valovi, koji se rasprostiru oko atomskih jezgra, stisnuti su električnim silama jezgre na malen prostor, a taj mali prostor rasprostiranja vala ispoljuje se u pokusu kao veličina atoma.