Spektar (fizika)



Spektar (lat. spectrum: pojava, priviđenje) je raspodjela intenzitetâ mjerene veličine prikazanih ovisno o nekoj fizikalnoj veličini, na primjer energiji, frekvenciji, brzini, masi i drugo.[1] Najčešće se pojam spektar koristi u značenju spektar elektromagnetskog zračenja. Kao analitičke funkcije energije u spektru elektromagnetskog zračenja koriste se:
- valna duljina je udaljenost između najbliže dvije točke iste elongacije i iste faze na valu:
- frekvencija je broj titraja koje neki val izvede u jedinici vremena:
- valni broj je broj valnih ciklusa u jedinici duljine:
gdje je: E - energija fotona, c - brzina svjetlosti, a h - Planckova konstanta.
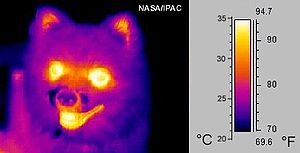
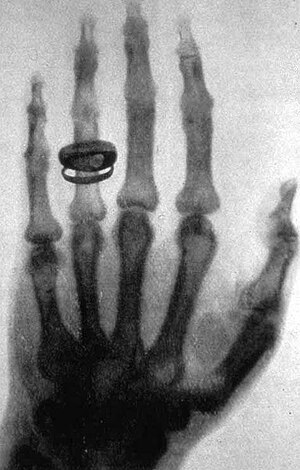
Elektromagnetski spektar prikaz je jakosti elektromagnetskoga zračenja kao funkcije njegove frekvencije, odnosno valne duljine. Obuhvaća sve vrste elektromagnetskih valova, od niskofrekventnih radiovalova (valne duljine od nekoliko kilometara) preko mikrovalova (30 cm do 1 mm) i područja optičkih spektara (infracrvenoga zračenja, vidljive svjetlosti, ultraljubičastoga zračenja; od 1 mm do 1 nm) do visokofrekvencijskoga rendgenskog zračenja (valne duljine do približno 1 pm) i gama-zračenja. Promjene u energijskim razinama elektrona odražavaju se uglavnom na ultraljubičastim i vidljivim spektrima, a od vibracijske i rotacijske energije molekula potječu infracrveni spektri.
| Elektromagnetski spektar | ||||
|---|---|---|---|---|
| Naziv | Valna duljina | Frekvencija (Hz) | Energija fotona (eV) | |
| Gama-čestica | < 0,02 nm | > 15∙1018 Hz | > 62,1 keV | |
| Rendgenske zrake | 0,01 nm – 10 nm | 30∙1018 Hz – 30∙1015 Hz | 124 keV – 124 eV | |
| Ultraljubičasto zračenje | 10 nm – 400 nm | 30 PHz – 750 THz | 124 eV – 3 eV | |
| Vidljiva svjetlost | 390 nm – 750 nm | 770 THz – 400 THz | 3,2 eV – 1,7 eV | |
| Infracrveno zračenje | 750 nm – 1 mm | 400 THz – 300 GHz | 1,7 eV – 1,24 meV | |
| Mikrovalovi | 1 mm – 1 m | 300 GHz – 300 MHz | 1,24 meV – 1,24 µeV | |
| Radio valovi | 1 mm – 100 km | 300 GHz – 3 kHz | 1,24 µeV – 12,4∙10-15 eV | |
Vidljivi spektar (koji zamjećuje ljudsko oko) odgovara nizu boja što nastaje rasapom bijele Sunčeve svjetlosti (disperzija; duga), od ljubičaste (valne duljine 380 nm), preko plave, zelene, žute i narančaste do crvene (780 nm).
Emisijski spektar koji nastaje raščlanjivanjem (na primjer s pomoću prizme ili optičke rešetke) emitiranoga zračenja užarenih tijela karakterističan je za fizikalna i kemijska svojstva izvora zračenja.
Apsorpcijski spektar nastaje raščlanjivanjem zračenja propuštenoga kroz tvari koje djelomično propuštaju a djelomično apsorbiraju elektromagnetsko zračenje na svojstven, selektivan način. Frekvencije zračenja koje neka tvar apsorbira odgovaraju frekvencijama koje bi ta tvar emitirala u usijanom stanju (Kirchhoffov zakon toplinskog zračenja). Čvrste tvari emitiraju kontinuirani spektar, koji sadrži sve frekvencije vidljivog, infracrvenog i ultraljubičastoga područja. Nasuprot tomu, tvari u plinovitom stanju emitiraju diskontinuirani, linijski ili atomski spektar, sastavljen od niza diskretnih monokromatskih spektralnih linija to jest samo zračenje frekvencija karakterističnih za pobuđeni atom. Rendgensko linijsko zračenje atoma nastaje kada upadni snop visokoenergijskoga zračenja izbija elektrone iz dijela elektronskog oblaka u blizini jezgre atoma a nastale se šupljine popunjavaju skokom elektrona iz viših energijskih razina. Tumačenje nastanka takvih spektara dovelo je do razjašnjenja strukture pojedinih atoma (kvantna mehanika), a na temelju proučavanja emisijskih spektara zvijezda razjašnjena su njihova fizikalna i kemijska svojstva (spektralni razredi zvijezda).
Spektri emisije, apsorpcije, raspršenja i polarizacije elektromagnetskoga zračenja primjenjuju se za objašnjenje strukture molekula, a služe i u kvalitativnoj i kvantitativnoj kemijskoj analizi. Razdvajanje spektralnih linija opaža se kad se promatraju spektri koje emitiraju ili apsorbiraju atomi u magnetskom ili električnom polju, a te se pojave nazivaju Zeemanov učinak ili Starkov učinak.
Druge vrste spektara se od elektromagnetskih spektara razlikuju po načelima energijskih promjena u ispitivanim tvarima ili načinu detekcije, na primjer spektar energijske razdiobe elektrona ili maseni spektar iona prema omjeru njihove mase i naboja, a također i magnetski spektar koji nastaje kada katodne zrake nakon prolaska kroz magnetsko polje padnu na odgovarajući zaslon, akustički spektar kao prikaz jest amplituda (ili faza) pojedinih komponenata složenoga zvuka kao funkcije frekvencije i drugo.
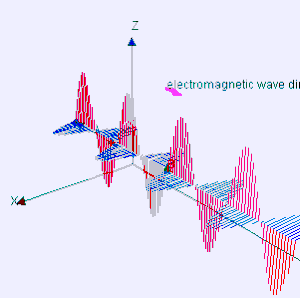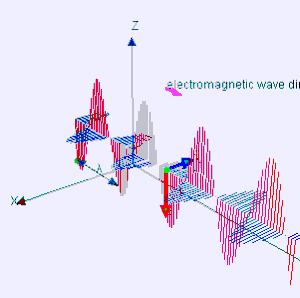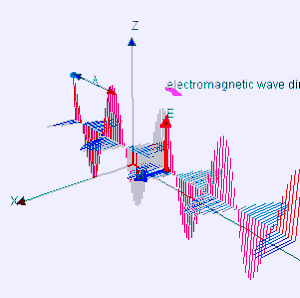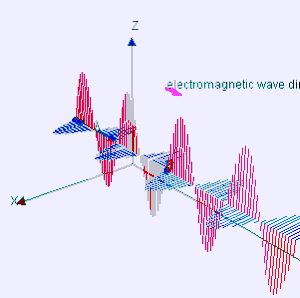
Valovi svjetlosti i elektromagnetski valovi imaju ista osnovna svojstva i šire se istom brzinom (brzina svjetlosti). Između njih nema nikakve razlike u njihovim fizičkim svojstvima, već se samo razlikuju u valnoj duljini, odnosno frekvenciji. Ogib, interferencija i polarizacija su pokazali da je svjetlost transverzalni val. Kod elektromagnetskog vala električno titranje je okomito na magnetsko, pa se te dvije promjene šire u prostor okomito na smjer svoga kretanja. Prema tome je i elektromagnetski val također transverzalno titranje. Pokusi pokazuju da električne promjene u elektromagnetskom valu djeluju na fotografsku ploču i na vidni živac u našem oku, pa imamo osjet svjetla. Sve nas to upućuje na to da su vidljivi valovi svjetlosti, kao i infracrvene, ultraljubičaste, rendgenske i gama zrake također elektromagnetski valovi, samo mnogo manje valne duljine. O valnoj duljini ovise njihova posebna svojstva. Svi valovi raspoređeni po svojoj valnoj duljini čine elektromagnetski spektar.
No sada se postavlja pitanje što je nosilac elektromagnetskih valova? Prije se smatralo da je nosilac tih valova neka hipotetična tvar, takozvani eter koji ispunjava čitav svemir. No, dalji razvoj znanosti odbacio je potpuno tu hipotezu. Ta bi, naime, tvar morala imati čudna svojstva, to jest ona bi morala biti savršeno kruta, a ipak bi se kroz nju gibala sva nebeska tijela bez ikakvog otpora. Osim toga morala bi biti i savršeno elastična. Danas se smatra da za elektromagnetske valove ne treba nikakav materijalni nosilac, i da su to samo periodičke promjene određenog fizičkog stanja u prostoru. Njihov je nosilac sam prostor, u kome se te promjene zbivaju.[2]












Užarena čvrsta tijela emitiraju svjetlost s kontinuirano raspodijeljenim valnim duljinama (toplinsko zračenje). Od temperature užarenog tijela zavisi koji je dio spektra najjači (najintenzivniji), ali od mjesta maksimuma postepeno se gasi svjetlost prema manjim i većim valnim duljinama. Nasuprot tome kontinuiranom spektru čvrstih tijela opaža se kod plinova i para nešto drugo. U njihovu se spektru pojavljuju diskretne linije, koje su svojstvene za pojedine kemijske elemente. Čitav spektar se sastoji od niza oštro određenih linija.
Lako je uvidjeti da linijski spektar potječe od atoma. Takvi se spektri dobivaju pri pokusima s katodnim i kanalnim zrakama. Električno izbijanje u katodnoj cijevi niskog tlaka izaziva uvijek velik broj atoma na emisiju svjetlosti. Linijske spektre emitiraju također i plemeniti plinovi, koji se sastoje od čistih atoma, a ne molekula.
Linijske spektre možemo studirati na emisijskom ili apsorpcijskom spektru. Pusti li se bijela svjetlost kroz neke pare ili plin, opaža se u dobivenom spektru da su neke valne duljine ugušene. Tamne linije stoje točno na onim mjestima spektra gdje bi ležale emisijske linije. Plin dakle apsorbira svjetlost onih valnih duljina koje bi inače emitirao. Apsorpcijski spektar slaže se potpuno s emisijskim. Ova određenost u spektrima kemijskih elemenata jedan je od temeljnih zakona nuklearne fizike.
Iako svakom kemijskom elementu pripadaju posebne, svojstvene spektralne linije, ipak se u njihovim spektrima opažaju neka zajednička svojstva, koja omogućuju da se unese red u golem spektroskopski materijal. Spektralne linije svakog kemijskog elementa daju se srediti u nekoliko serija. Svaka pojedina serija predstavlja niz linija koje su poredane po određenom pravilu. Često se već na prvi pogled vidi da linije jedne serije pripadaju zajedno. Promatramo li linije od većih valnih duljina prema manjim, udara nam odmah u oči da se razmak između njih smanjuje. Linije se gomilaju prema određenoj valnoj duljine, koja je granica te serije.
Prvi je J. J. Balmer 1885. otkrio da se vodikov spektar može prikazati jednostavnom matematičkom jednadžbom. Njemu su tada bile poznate 4 vidljive vodikove linije s valnim duljinama:
- Hα = 656, 199 nm
- Hβ = 486, 152 nm
- Hγ = 434, 067 nm
- Hδ = 410, 194 nm
Običaj je da se vodikove linije označe početnim slovima grčkog alfabeta, koja dolaze kao indeksi kemijskom simbolu H. Recipročne vrijednosti valnih duljina tih četiriju linija daje se jednadžbom (Rydbergova formula):
gdje je: m = 3, 4, 5, 6; a R je takozvana Rydbergova konstanta. Uvrstimo li u Balmerovoj jednadžbi za m cijele brojeve veće od 7 dobivamo valne duljine koje leže u ultraljubičastom području spektra. Pokusima se doista našlo još oko 30 linija koje se potpuno slažu s Balmerovom jednadžbom. Linije se gomilaju prema valnoj duljini koja je dana izrazom:
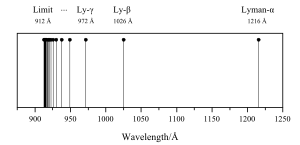
To je granica serije. Balmerova serija je idealni tip spektralnih linija uopće. Kako se vidi na slici, razmak između susjednih linija pravilno se smanjuje, i linije se gomilaju prema određenoj granici.
Iz razloga koji će se kasnije iznijeti uvedeno je da se spektralne jednadžbe postavljaju za frekvencije, a ne za valne duljine. Pokusima se, doduše, mjere valne duljine (iz interferentnih, ogibnih ili disperzionih pojava), ali zakoni spektralne analize postaju pregledniji kad se uzimaju u obzir frekvencije. Pri tom treba misliti na sljedeće: frekvencija ν se može izračunati iz valne duljine λ prema poznatom odnosu:
No brzina svjetlosti c nije tako točno izmjerena kako su točna mjerenja valne duljine. Točnost spektralne analize je nenadmašiva. Iz tog razloga i dalje se u spektralnoj analizi svi iskustveni podaci izražavaju u valnim duljinama.
Uvodeći frekvenciju, možemo Balmerovu jednadžbu pisati u obliku:
gdje je m = 3, 4, 5…. Frekvencije spektralnih linija vodika mogu se dakle prikazati kao razlike (diferencije) između dva člana, od kojih je prvi konstantan, a drugi opada kao 1/9, 1/16, 1/25, 1/36 …. Tu se odmah nameće pitanje: Mora li se uvijek uzeti kao konstantan broj 1/4? Moguće je pomisliti, da prvi konstantni član bude bilo koji razlomak 1/n2. Godine 1908. našao je F. Paschen u infracrvenom području spektralne linije vodika kojima su se valne duljine točno slagale s izrazima:
Tu dakle imamo dva člana jedne serije, kojoj je konstantni član R/32. Taj član ujedno određuje i granicu serije. I od te takozvane Paschenove serije nađen je vrlo velik broj linija. Godine 1916. pronašao je Lyman na drugoj strani od Balmerove serije, duboko u ultraljubičastom području, nove spektralne linije, koje smo mogli prikazati istom Balmerovovom jednadžbom, samo što je za konstantni član trebalo uzeti u nazivniku cijeli broj 1. Vodikov spektar sastoji se, od ovih serija:
Lymanova serija:
gdje je: m = 2, 3, 4 ….
gdje je: m = 3, 4, 5 ….
Paschenova serija:
gdje je: m = 4, 5, 6 ….
Brackettova serija:
gdje je: m = 5, 6, 7 ….
Pfundova serija:
gdje je: m = 6, 7, 8 ….
Od tog golemog mnoštva linija padaju u vidljivo područje spektra svega prve 4 linije Balmerove serije. Odatle se vidi kako je važno ispitivati čitav spektar da se nađu osnovni zakoni serije.
Frekvencije spektralnih linija vodika možemo općenito izraziti jednadžbom:
gdje su: n i m - cijeli brojevi.
Frekvencije vodikovih linija dobiju se, dakle, da se od niza c∙R/n2 učine sve moguće pozitivne razlike (diferencije). Tako objašnjena, Balmerova jednadžba vodi nas do općeg načela kombinacije, što ga je otkrio W. Ritz 1908. Po tom načelu dade se za svaki kemijski element postaviti niz terma T1, T2, T3, …. tako da su frekvencije njegova spektra dane razlikama (diferencijama):
Ritzovo načelo kombinacije potvrđeno je pri ispitivanju svih spektara. Ono je ključ za sređivanje različitih serija. Načelo kombinacije sadrži u sebi osnovni zakon prirode, koji se u punom smislu razotkriva tek u nuklearnoj fizici.
Kakve bismo spektre očekivali po klasičnoj teoriji? Razmotrimo najjednostavnije primjer, vodikov atom. Jedan elektron kreće se oko protona. U najjednostavnijem slučaju staza elektrona je kružnica. Gibanje elektrona u kružnici predstavlja pravilno harmonično titranje. Po klasičnoj teoriji elektromagnetsko polje oko atoma titra isto tako kao i elektron. Prema tome bi atomi emitirali svjetlost s frekvencijama koje bi se točno podudarale s frekvencijama titranja elektrona. No prema poznatom trećem Keplerovom zakonu frekvencija gibanja čestice dana je promjerom staze. Elektron se, naravno, u klasičnoj teoriji može okretati u bilo kojoj kružnici oko protona. Odatle izlazi, da bi mnoštvo vodikovih atoma emitiralo svjetlost sa svim mogućim frekvencijama. Upotpunimo još ovu sliku time da se elektroni kreću i u eliptičnim stazama. Tada njihovo gibanje nije više harmoničko. S druge strane, ono je i dalje periodičko i po Fourierovu teoremu može se prikazati kao beskrajna suma harmoničkih titranja s frekvencijama ν0, 2∙ν0, 3∙ν0, ….. gdje ν0 znači frekvenciju titranja elektrona oko jezgre. Kao i kod zvuka, tako bismo i ovdje očekivali pored osnovnog "tona" i "gornje tonove". Spektar vodikova atoma sastojao bi se, dakle, od beskrajnog mnoštva linija, koje bi imale među sobom jednaki razmak. Treba istaći da ovaj zaključak vrijedi i za složene atome i on se ne da izbjeći, ma kako proizvoljno odabrali model atoma.
Zakoni spektralne analize stoje u neizgladivoj suprotnosti s klasičnom teorijom. Iz tih suprotnosti rodila se moderna nuklearna teorija.
Ne protivi se klasičnoj fizici samo izgled optičkih spektara, nego i isto tako čudesna stabilnost atoma. Atomi nekog kemijskog elementa jednaki su. Oni imaju jednaka svojstva. Ta stabilnost atoma koja se prije činila prirodnom nije više sama po sebi razumljiva, otkako znamo da su atomi sastavljeni. Po klasičnoj teoriji elektron se može kretati u bilo kojoj elipsi koja ima žarište u jezgri. Prema tome bi se i atom u svakom pokusu pokazivao s drukčijim svojstvima. Međutim, mjesto te posvemašnje raznolikosti, koju bismo očekivali po klasičnim zakonima, u prirodi se pojavljuju atomi nekog kemijskog elementa s uvijek istim fizičkim i kemijskim osobinama. Ta čudesna stabilnost mikrosvijeta ukazuje nepobitno na granice klasične fizike.
Zamislimo načas da smo nekim vanjskim zahvatima uspjeli ostvariti u mnoštvu vodikovih atoma jednaka gibanja elektrona. U taj čas, naravno, svi su vodikovi atomi jednaki. Što će se dalje dogoditi? Shvatimo li atom kao klasični sistem, tad bismo vanjskim utjecajima mogli kontinuirano mijenjati oblik elipse elektrona. Gomilanjem sitnih vanjskih utjecaja s vremenom bi se znatno izmijenilo prvobitno stanje atoma; prvobitne jednakosti bi nestalo. No u stvarnosti to se ne događa. Atomi ostaju jednaki i tada kad se neprestano srazuju, kao u plinu. U svijetu atoma moraju biti na neki način postavljene granice principu kontinuiranog mijenjanja.
Isto tako nerazumljiva je u klasičnoj fizici osnovna činjenica da atomi u svojim stabilnim stanjima ne emitiraju svjetlost. Prema Rutherfordovu modelu morao bi se elektron stalno kretati oko jezgre, jer bi inače pao na nju. No svako ubrzano ili usporeno gibanje je po Maxwellovoj teoriji praćeno elektromagnetskim valovima. Želimo li dakle zadovoljiti klasičnu mehaniku, ogrešujemo se odmah o elektrodinamiku.
Stabilnost atoma, kao i emisiju i apsorpciju svjetlosti, možemo razumjeti samo onda ako u te procese unesemo osnovnu diskontinuiranost koju je M. Planck otkrio u zračenju crnog tijela. Planck je pretpostavio da harmonički oscilator može poprimiti samo diskontinuirane vrijednosti energije. A. Einstein je išao još korak dalje s hipotezom da se svjetlost sastoji od kvanta energije h∙ν. Ako je ta hipoteza točna, tad atomi mogu samo trenutno, u izvjesnim kvantnim skokovima, emitirati ili apsorbirati svjetlost. Emisija i apsorpcija svjetlosti tada je diskontinuiran proces, s jedne strane zato što atom ne može kontinuirano mijenjati svoju energiju, a s druge strane zato što atom emitira svjetlost kao kvant energije.
Poopćivši Planckovu hipotezu diskontinuiranosti, postavio je N. Bohr za osnov kvantne teorije ove postulate:
- Atomi mogu boraviti samo u određenim stacionarnim stanjima koja se među sobom oštro razlikuju. Prepušteni sami sebi, nalaze se atomi u stabilnom stanju, to jest u stanju najniže energije. Izvanjskim utjecajima možemo atome prevesti samo u stacionarna stanja više energije. Za to potrebna energija jednaka je razlici energije stacionarnih stanja.
- Nalazi li se atom u nekom pobuđenom stacionarnom stanju, on prelazi sam od sebe u stacionarno stanje niže energije emitirajući pri tom kvant svjetlosti. Energija kvanta svjetlosti jednaka je razlici (diferenciji) između energije višeg i nižeg stacionarnog stanja.
Energiju stabilnog stanja atoma označit ćemo s E1, drugog stacionarnog stanja s E2, trećeg s E3 i tako dalje. Pri prijelazu iz stacionarnog stanja s energijom En u stacionarno stanje Em atom emitira kvant svjetlosti energije:
Odatle izlazi za frekvenciju svjetlosti izraz:
Ova jednadžba predstavlja drugi Bohrov postulat, koji stoji u potpunoj paraleli s iskustveno potvrđenim Ritzovim načelom kombinacije. Prema iskustvu, frekvencije spektralnih linija mogu se prikazati razlikama (diferencijama) dvaju terma iz niza T1, T2, T3, …., Isto to veli i drugi Bohrov postulat. Prema tome se spektralni termi moraju podudarati s energijama atoma. Ovo stajalište otvara sasvim novi vidik na zakonitosti spektralne analize.
Bohrovim postulatom zadobio je Ritzovo načelo kombinacije temeljno fizičko značenje. Prikazivanje frekvencija kao razlika spektralnih terma drugi je oblik Bohrov postulat. Negativni umnožak spektralnog terma s Planckovom konstantom jednak je energiji pojedinog stacionarnog stanja atoma:
U iskustvenom zakonu spektroskopije već je davno prije postanka kvantne teorije izrečen temeljni zakon nuklearne fizike. Skupivši i vrlo točno odredivši odredivši spektralne terme atoma, spektroskopičari su tim samim skupili mnoštvo zakona o energijama atoma. Na osnovu spektroskopskog materijala mogu se najtočnije odrediti atomske diskretne energije, a to određenje energija iz spektralnih terma premašuje samu astronomsku točnost.
Emitirane frekvencije mogu se vrlo pregledno prikazati grafičkom slikom u kojoj su energije stacionarnih stanja atoma nanesene kao vodoravne paralelne linije. Udaljenošću između dvaju energetskih nivoa određen je umnožak između frekvencije i Planckove konstanta. Balmerovoj seriji odgovaraju prijelazi iz viših energetskih nivoa na drugi energetski nivo odozdo. Veličine strelice koje označuju prijelaz proporcionalne su emitiranim frekvencijama. Prijelazi na najniži energetski nivo daju frekvencije koje leže u ultraljubičastom. Najveća frekvencija tih prijelaza dana je prijelazom atoma iz najvišeg stacionarnog stanja u stabilno stanje. Taj proces nastaje na primjer kad proton uhvati koji slobodan elektron u svojoj okolini. Frekvencije svjetlosti emitirane prilikom prijelaza u treći energetski nivo, n = 3, leže u infracrvenom dijelu spektra. Isto tako, naravno, vrijedi i za prijelaze k ostalim višim energetskim nivoima. Od mnoštva vodikovih spektralnih linija samo četiri linije padaju u vidljivi dio spektra.
Mi smo dosad promatrali samo spontane prijelaze iz energetskih viših stacionarnih stanja u niža uz emisiju kvanta svjetlosti. Obrnut proces od toga je apsorpcija. Poznata je činjenica da atomi apsorbiraju svjetlost samo onih frekvencija koje inače mogu emitirati. Obasjavamo li vodikove atome svjetlošću koja ima frekvenciju upravo jednaku razlici (diferenciji), c∙R - c∙R/22, c∙R - c∙R/23 ili c∙R - c∙R/24, to mogu vodikovi atomi prijeći iz stabilnog stanja u prvo, drugo ili treće pobuđeno stacionarno stanje. Energije kvanata svjetlosti upravo su tako velike da atomi, apsorbiravši ih, prelaze iz stabilnog stanja u energetski viša stanja. Ako je energija kvanta veća ili manja od tih energija, tada se ne opaža apsorpcija svjetlosti. U stabilnom stanju ne mogu na primjer vodikovi atomi apsorbirati 4 vidljive Balmerove linije. Energija kvanata te svjetlosti ne dostaje da atom prevedemo iz stabilnog u koje pobuđeno stanje. U stabilnom stanju vodikovi atomi apsorbiraju samo ultraljubičaste Lymanove linije. Podudaranje između emisijskog i apsorpcijskog spektra najbolja je potvrda kvantnoteorijskih predodžbi o emisiji i apsorpciji atoma.
Atomi mogu apsorbirati kvante svjetlosti kada se nalaze i u kojem višem energetskom nivou. Ako je na primjer atom prešao apsorpcijom u prvi pobuđeni energetski nivo, tada može ponovnom apsorpcijom kvanta svjetlosti prikladne energije prijeći u drugi pobuđeni energetski nivo. Za ta dva skoka potrebna je svjetlost dviju frekvencija, kod vodika na primjer c∙R i c∙R/22 - c∙R/23. U isto vrijeme ćemo, dakle, atome obasjavati svjetlošću koja ima te dvije frekvencije. Atomi koji su prešli u energetski viša stanja vraćat će se u stabilna stanja. Iz drugoga pobuđenog stanja može atom prijeći ili direktno u stabilno stanje ili najprije u prvo pobuđeno stanje. U drugom slučaju emitira atom iste frekvencije svjetlosti koje je i apsorbirao. U prvom slučaju, naprotiv, emitira atom svjetlosti koja ima frekvenciju jednaku sumi iz frekvencija apsorbiranih svjetlosti. Pojavljivanje tih triju spektralnih linija opaža se zaista u pokusu i ono govori vrlo uvjerljivo u prilog kvantnog shvaćanja atomskih procesa. Samo u okviru kvantne teorije dade se shvatiti da atom može emitirati svjetlost s frekvencijom jednakom sumi frekvencija svjetlosti koje je prethodno apsorbirao.
Kvantnom teorijom našle su jednostavno tumačenje vrlo zanimljive pojave fluorescencije. Obasjavamo li neke tvari svjetlošću, opažamo da atomski sistemi mogu apsorbiranu energiju djelomično ili sasvim emitirati u obliku svjetlosti. Pomislimo da smo kemijsku tvar obasjavali monokromatskom svjetlošću. U mnogo slučajeva tvari zrače opet svjetlost s tom istom frekvencijom kakvu ima svjetlost obasjavanja. Međutim je češće da tvar emitira svjetlost s frekvencijama različitim od prvotne apsorbirane svjetlosti. Za te frekvencije vrijedi Stokesovo pravilo da su emitirane frekvencije uvijek manje od frekvencije svjetlosti kojom smo obasjavali tvar. Tako na primjer može tvar zračiti crvenu svjetlost, iako je prije bila obasjana plavom (modrom). Prema kvantnoj teoriji možemo tu pojavu lako obasjasniti. Atomski sistemi ne vraćaju se izravno u prvotna stabilna stanja, već po izvjesnim okolišnim putovima, pa se prvotna energija apsorbiranog kvanta svjetlosti razdijeli u više manjih doza energije, koje se postepeno emitiraju.[3]
- ↑ spektar, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2016.
- ↑ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.
- ↑ Ivan Supek: "Nova fizika", Školska knjiga Zagreb, 1966.



















