Apolonijeva mreža
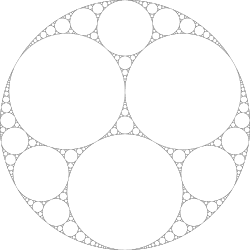
Apolonijeva mreža ili Apolonijev skup je fraktal sastavljen od kružnica. Dobio je ime po grčkom matematičaru Apoloniju, a fraktalna mu se dimenzija procjenjuje na 1.3057.

Počnimo s trima kružnicama, A, B i C, od kojih svaka dodiruje preostale dvije te docrtajmo još dvije kružnice, D i E, koje dodiruju svaku od početnih kružnica. Te se dvije kružnice zovu Apolonijeve kružnice (vidi Descartesov teorem. Uzmimo sad jednu od docrtanih kružnica, npr. E, i promatrajmo ju u skupu s dvije od prve tri kružnice, npr. A i C. Te tri kružnice također imaju svoje Apolonijeve kružnice – jedna je kružnica B, a drugu označimo slovom F. Isto možemo učiniti s trojkom ABE, dobivajući kružnicu G, te s BCE, dobivajući H. Nastavljamo s trojkama ABD, ACD i BCD dobivajući nove tri kružnice. Postupak se ponavlja sa svim trojkama kružnicâ koje zadovoljavaju svojstvo iz prve rečenice. Skup kružnica koji se dobije nakon beskonačnog broja ponavljanja naziva se Apolonijeva mreža.
Nakon svake iteracije nastaje novih kružnica. Ako kao nultu iteraciju označimo prvih pet kružnica, nakon n-te iteracije dobijemo kružnica.

Počinjemo četirima sferama od kojih svaka dodiruje preostale tri. Postoje još dvije sfere koje imaju svojstvo da dodiruju svaku od početnih sfera – jedna "između", a druga "izvan" njih. Nastavljamo kao kod dvodimenzionalne Apolonijeve mreže – za svaku četvorku sferâ koje se dodiruju dodamo još dvije, i tako u nedogled. Fraktalnu su dimenziju izračunali M. Borkovec, W. De Paris i R. Peikert[1] te ona iznosi otprilike 2.4739.


